TEXSTAN

Institut für Thermodynamik der Luft- und Raumfahrt - Universität Stuttgart
Mechanical Engineering - The University of Texas at Austin

TEXSTAN Glossary of Terms - definitions and explanations

This section contains terms that are often used in convective heat, mass, and momentum transfer. The section variables presents definitions of the flags and variables that appear in an input dataset. Definitions of the variables that appear in the output files are found in external flows: output files and internal flows: output files sections of this website.

A B C D E F G H I J K L M N O P–Q R S T U V W X Y–Z

A top of page

accelerating flow: For external flows, see favorable pressure gradient. For internal subsonic flows acceleration is most often caused by a decrease in flow cross-sectional area.

adiabatic wall temperature

The adiabatic wall temperature is often called the recovery temperature. In TEXSTAN for variable property flows, the user can choose to base the heat transfer coefficient on either the stagnation temperature or the adiabatic wall (or recovery) temperature. 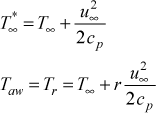The default value is stagnation temperature, and input flag k2 switches the choice to the adiabatic wall temperature, (T_s - T_aw), where the stagnation temperature and adiabatic wall (or recovery) temperature definitions are recovery temperataure

The recovery factor, r, for k2=1 is based on whether the flow is laminar or turbulent, r = Pr^1/2 for laminar flow (mode=1) and r = Pr^1/3 for turbulent flow (mode=2). For k2=3 the recovery factor is fixed at r = 0.892.

Note: that the adiabatic wall temperature for the case of a three-temperature potential heat transfer problem (gas turbine film cooling applications) has a completely different definition.

adverse pressure gradient: In boundary layer flows, an adverse pressure gradient is caused by the free stream velocity decelerating (or decreasing) in the flow direction, leading to a pressure field that increases in the flow direction. As the flow attempts to move into a region of higher pressure, the thickness of the boundary layer will tend to increase to engulf more free stream kinetic energy to overcome the increasing flow-work energy, and this in turn leads to a significant decrease in wall shear stress. If the adverse pressure gradient is strong enough, the flow will eventually separate from the surface. The numerics in TEXSTAN are such that flow calculations can not be carried out beyond the separation point, and TEXSTAN will abruptly terminate.

approach flow: In external flows, the approach flow is a term used to describe the flow approaching a body (for example, a flat plate or a turbine blade or vane). The velocity of the approach flow is often used to normalize variables such as pressure coefficients or turbulence intensity.

B top of page

benchmark data set: TEXSTAN uses benchmark data sets (test cases) for three main purposes: the first is to teach the user how to set up various types of external and internal flow problems; the second is to test or check the compiled version of TEXSTAN to make sure nothing has changed; and the third is to demonstrate that, at least for these test cases TEXSTAN validates against acceptable momentum, heat, and mass transfer correlations and/or data in the open literature.

Blasius problem: The Blasius problem is the classic Prandtl laminar boundary layer problem. For the momentum part of the Blasius problem, the free stream velocity u_∞ = constant, and for the heat transfer part of the Blasius problem, the surface temperature T_s = constant. The Blasius problem is also called the flat plate problem, the zero-pressure-gradient problem, or the Falkner-Skan m=0 problem.

blowing: For external flows, blowing is the injection of low-momentum transfer of fluid through a surface and into the boundary layer. Blowing can be used as a means to reduce high heat flux rates, for example near the throat of a supersonic nozzle. Blowing is described in more depth in the glossary entry transpiration.

boundary layer approximations: TEXSTAN is designed to solve two-dimensional flows that obey the momentum boundary layer approximations. There are traditionally four requirements for the flowfield. The first three requirements are grouped together: the streamwise velocity component (u) must be much larger than the cross-flow velocity (v) and its inline and cross derivatives must all be small:
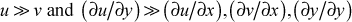
This requires the surface to be continuous and contain no forward- or backward-facing steps, and the surface must not be subjected to a strong adverse pressure gradient (occurring in the downstream section of a converging-diverging nozzle or near the trailing edge of an airfoil or turbine blade). The flow geometries that obey the boundary layer approximations are described by the input variable kgeom. The final momentum boundary layer approximation is that the pressure gradient be one-dimensional, P(x). This requirement restricts the strength of the surface axial curvature, because the TEXSTAN boundary layer equations do not include this effect. The energy equation boundary layer approximation is that the temperature gradient in the cross-stream direction be much larger than its gradient in the flow direction, and this approximation is generally never violated.

boundary layer thickness: The primary use of the boundary layer thickness is to determine the outer-layer length scale in the mixing-length model of turbulence (see modeling: mixing length model section of this website). For external flows the boundary layer thickness δ₉₉ is the edge of the boundary layer where (u/u_∞)=0.99. This value is formulated to exclude localized maximums within the boundary layer. For internal flows, the boundary layer thickness is defined differently. For pipe flow (kgeom=4) it is the wall radius, for parallel-plane channel flow (kgeom=5,6) it is the channel half height, and for annular flow (kgeom=7), it is arbitrarily set equal to the average of the inner and outer radius.

bulk temperature: This term is synonymous with mass-averaged temperature.

C top of page

Chilton-Colburn analogy: See Reynolds analogy.

combined entry flow: A combined entry flow is an internal flows where heat transfer begins at the entrance to the duct or channel. The typical assumption is that the flow entrance shape is smooth enough and convergent enough to cause the velocity profile to accelerate sufficiently such that it becomes approximately flat. Generally, a flat profile is also a good approximation for all scalar properties of the flow, such as temperature, turbulence kinetic energy, and turbulence dissipation at the entrance. For the momentum problem this flat-profile starting condition yields an infinitely large wall shear stress and pressure gradient. Similarly, if the applied surface thermal boundary condition is a specified wall temperature (the Dirichlet problem) and the applied surface temperature is different from the fluid entry temperature, the initial surface heat flux will also be infinite in magnitude at the entrance.

constant properties: For external flows the constant properties assumption for gases requires the ratio of free stream static temperature to wall temperature to be in the range 0.90 ≤ (T_s / T_∞) ≤ 1.1 and for liquids the ratio reduces to the range 0.95 ≤ (T_s / T_∞) ≤ 1.05. For internal flows the free stream temperature is replaced by the mass-averaged (mean) temperature, T_m , and the same general rules apply. See also variable properties.

Convective Heat and Mass Transfer, 4th ed. - CHMT: TEXSTAN has been designed to accompany the graduate-level textbook Convective Heat and Mass Transfer, (currently 4th ed., McGraw-Hill, 2005, by William M. Kays, Michael E. Crawford, and Bernhard Weigand). This textbook presents a strong theoretical basis for the subject of convective heat and mass transfer by focusing on boundary layer theory, while encouraging the use of a numerically-based computational approach to solving problems in parallel with classical problem-solving approaches.

D top of page

decelerating flow: For external flows, see adverse pressure gradient. For internal flows deceleration is most often caused by an increase in flow cross-sectional area.

displacement thickness: The displacement thickness for planar flow is evaluated from the integral
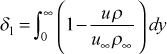
The displacement thickness is found to be strongly dependent on density variation, so it is primarily useful for incompressible flows. The displacement thickness is typically incorporated into Euler equation solutions to account for streamline displacement, and this correction provides a better approximation to the free stream velocity distribution over airfoil and turbine blade surfaces. Some turbulence models have made use of a Reynolds number based on the displacement thickness, but this concept is not used in TEXSTAN. Corrections to this integral for transverse curvature is described in the external flows: Reynolds number section of this website.

E top of page

E-surface: The I-surface entry contains both definitions.

enthalpy thickness: The enthalpy thickness for planar flow is evaluated from the integral
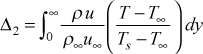
It is the natural variable that arises when the boundary layer stagnation enthalpy equation is partially integrated in the cross-stream direction to form an integro-differential equation called the energy integral equation, and it's streamwise derivative is seen to be directly proportional to the nondimensional surface heat transfer coefficient (just as the momentum thickness streamwise derivative is directly proportional to the nondimensional surface shear stress). These equations are addressed in depth in our textbook, CHMT. Corrections to this integral for transverse curvature is described in the external flows: Reynolds number section of this website.

entrainment: Entrainment is mass flux through the E-surface (the free surface) of external flow problems, and it is iteratively computed within TEXSTAN to maintain near-zero gradients of the dependent variables at that surface as the boundary layer displacement thickness changes the position of the streamlines. For internal flows, the streamlines are bound between fixed positions (the I- and E-surfaces, which are not permitted to move in physical space), and the total mass flow rate is equal to the inflow mass flow rate. No additional fluid is permitted to enter through either the I-surface or the E-surface. Entrainment control and entrainment theory of external flows are discussed in detail in their respective sections of the external flows: integration control section of this website.

external flow: TEXSTAN considers only two flow classes: internal (or channel) flows and external flows (currently TEXSTAN does not handle free-shear flows). For both internal and external flows, the boundary layer approximations require specification of the pressure gradient, dP/dx, to mathematically close the set of equations. For the external flow class the pressure gradient is specified via the streamwise-direction distribution of the free stream velocity distribution u_∞ (x), and then the local pressure gradient is calculated using Euler's streamline-direction equation for inviscid fluid motion, ignoring axial-direction surface curvature. In TEXSTAN the external flow geometries include flow over a flat plate or wedge, flow over a turbine blade or vane, flow over a body of revolution such as a cylinder or sphere or missile-shaped surface, and flow in converging-diverging ducts that are either two-dimensional or axisymmetric in cross-section.

F top of page

Falkner-Skan flow

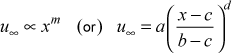
A Falkner-Skan flow is an external flow with a pressure gradient in which the free stream velocity u_∞ (x) is proportional to x^m. Falkner-Skan uinf(x)
where a is the approach velocity, b is a distance scaling factor, c serves as a virtual origin, and d is the Falkner-Skan variable m.

For m>0 the flow accelerates in the flow direction, leading to a favorable pressure gradient over the surface, and for m<0 the flow decelerates, leading to an adverse pressure gradient. Classical fluid mechanics similarity solution techniques are used to solve the Falkner-Skan problem, yielding a set of analytical expressions for such items as boundary layer thickness parameters, wall friction, and velocity profiles. The Falkner-Skan class of self-similar flows are often used to test boundary layer computer programs, and a number of TEXSTAN's benchmark datasets are based on this class of flows. Note that the classic Blasius problem is a subset of the Falkner-Skan problem for m=0, leading to u_∞ = constant, and thus no pressure gradient over the surface. The classic 2-D stagnation point flow is also a subset of the Falkner-Skan problem for m=1 (b=1 and c=0), leading to u_∞ directly proportional to x, and thus a good approximation of the velocity flow field on the leading edge of a cylinder in crossflow and on the leading edge of a typical turbine blade design.

favorable pressure gradient: In boundary layer flows, a favorable pressure gradient is caused by the free stream velocity accelerating (or increasing) in the flow direction, leading to a pressure field that decreases in the flow direction. By nature of the fluid flow physics all flows easily move into a region of lower pressure, and often the boundary layer thickness decreases. The numerics in TEXSTAN are not significantly affected by acceleration.

finite difference mesh: The finite difference mesh - or grid - is created using the initial velocity profile, u(y), and the same distribution of y locations is used for the other dependent variables. The details of establishing the mesh is described in the overview: numerical accuracy section of the website.

flat plate problem: The flat plate problem is the classic Prandtl boundary layer problem or Blasius problem. The origin of the name relates to potential flow where parallel streamlines approaching an infinitely thin flat plate do not change direction, implying the velocity vector tangent to each streamline stays constant in both magnitude and direction. The magnitude of the velocity vector is the free stream velocity u_∞ = constant, and its magnitude matches the approach flow velocity magnitude. Note that in real flows, streamlines that flow over a flat plate do slightly change direction or diverge, called the displacement thickness effect. The experimental implication of this fact is that the flow field over a flat plate has to be carefully controlled to maintain u_∞ = constant from the beginning of the plate to the end of the plate.

forced convection: A forced convective flow in TEXSTAN can occur in either over an external geometry such as a flat or axisymmetric surface or within an internal geometry such as a channel of circular, high aspect ratio rectangular or annular cross-section. In CHMT we define forced convection as fluid motion derived from some external means such as pumps, blowers, wind, vehicle motion, and so forth. For both classes of flow geometry, a pressure gradient is the primary driver of the flow. For external flows, the pressure gradient is applied by way of the free stream velocity boundary condition. For internal flows, the user specifies the inlet pressure and the fluid mass flow rate (by way of the initial velocity profile), and the resulting exit pressure will then depend on the channel length. For either class of geometry TEXSTAN can add additional body forces to either aid or oppose the flow, but the flow Reynolds number must always be sufficiently high that the customary boundary layer approximations are valid.

free convection

A free convective boundary layer flow in TEXSTAN is an external flow over a flat surface that is driven purely by a free-convective or buoyancy body force. The free stream velocity over the surface is zero, i.e. there is no applied pressure gradient (equivalent to the Blasius flat plate problem). Technically a free convective flow is a natural convective flow in which there are no surrounding surfaces to disturb the flow field from being primarily two-dimensional. The strict requirement for a free convective flow to occur is that there must be some component of the gravitational force vector perpendicular to the density gradient within the fluid over the surface. The density gradient is caused either by controlling the surface temperature such that the surface is colder than the surrounding fluid or such that the surface is hotter than the surrounding fluid.

The body force per unit volume for free convective flows is ρg, where ρ is the fluid density and g is the local gravitation. Its sign convention is plus if the direction of action of g is in the +x flow direction and minus if the direction of action of g is in the -x direction. For example, to calculate flow on a heated vertical flat plate where the buoyancy force would cause fluid to flow upward along the plate, the direction of the gravitational force would be in the opposite (-x) direction, and the input to TEXSTAN for g would equal either -9.8 m/s² or -32.17 ft/s² (depending on whether the user has chosen SI or US Customary units).

free stream pressure: See pressure.

free stream temperature: See temperature.

friction coefficient: The friction coefficient, c_f , is the classical Fanning friction coefficient. It is the conventional term used in fluid mechanics to represent the surface friction that is nondimensionalized using flow transport variables. For external flows see the external flows: friction section of this website, and for internal flows see the internal flows: friction section of this website. Note that it is customary in TEXSTAN to present external flow friction data in terms of c_f /2 in keeping with the classical formulation of the integral equation for momentum, rather than using c_f .

friction factor: The friction factor, f, is the classical Moody friction factor. It is the conventional term used in fluid mechanics for computing pressure drop in a pipe or channel, and it is four times larger than the friction coefficient for internal flows, f = 4 c_f - see the internal flows: friction section of this website.

G top of page

grid: The grid - or finite difference mesh - is created using the initial velocity profile, u(y), and the same distribution of y locations is used for the other dependent variables. The details of establishing the mesh is described in the overview: numerical accuracy section of the website.

H top of page

heat transfer coefficient: The heat transfer coefficient, h, is the ratio of the surface heat flux to a temperature driving potential (surface temperature to reference temperature difference). The reference temperature for external flows is the free stream for constant property flows, and it is either the stagnation temperature or the adiabatic wall (recovery) temperature for variable property flows - see the external flows: heat transfer section of this website. For internal flows the reference temperature is the mass-averaged temperature - see the internal flows: heat transfer section of this website.

high speed flow: A high speed flow is typically a flow with a Mach number greater than about 0.4. To properly model the high speed flow the energy equation must be solved to capture the effect of variable properties caused by viscous dissipation (viscous work effect). The variable properties flag kfluid is set > 1 (appropriate to the fluid of choice) and the viscous dissipation flag is activated by setting jsor(j) =3 for the energy equation.

hydraulic diameter

For internal flows the hydraulic diameter, D_h , is the customary length scale in forming a Reynolds number to predict whether the flow will be laminar or turbulent far from the entrance of the pipe or channel. The hydraulic diameter Reynolds number and the associated hydraulic diameter is defined as

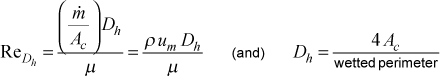
The variable A_c is the flow cross-sectional area, and the variable u_m is the mass-averaged velocity (which is the same as the mean velocity). The wetted perimeter depends on the flow cross-sectional area: for a pipe it will be the circumference, and for an annulus it will be the sum of the inner circumference and the outer circumference.

For a flat duct (sometimes called a parallel planes duct) the perimeter can be defined as two times the duct (or parallel planes) spacing plus two times a "large" variable that represents the width of the parallel planes, say L, which is theoretically infinite in length. When the ratio of cross-sectional area to wetted perimeter is formed, terms will form where L is in the denominator, and in forming the limit as L goes to infinity, those terms will vanish. For the flat duct the area-perimeter ratio becomes (L x a)/(2L + 2a) = (a)/(2 + 2a/L) = a/2, leading to a hydraulic diameter of 2a.

hydrodynamic entry length: The hydrodynamic entry length is the distance from the entrance of a channel to the point where the flow becomes hydrodynamically fully developed. Typically the entry length is defined when the four characteristics of the fully developed condition are achieved to within a certain percentage, typically to within five percent or smaller. These four characteristics include: (a) the surface shear stress begins with an infinite magnitude and decreases, approaching a constant value by the end of the entry region; (b) the axial pressure gradient similarly begins with an infinite magnitude and decreases, approaching a constant value by the end of the entry region; (c) the flow radial velocity (axisymmetric flows) or transverse velocity (planar flows) begins with a zero magnitude, then increases, and finally decreases, approaching zero at all cross-stream locations by the end of the entry region; and (d) the non-dimensional axial velocity profile (the axial velocity profile normalized by the mass-averaged velocity) begins with a flat profile and changes to a profile of constant, non-changing shape by the end of the entry region. A requirement for hydrodynamically fully-developed flow is that fluid properties remain approximately constant, which means the flow must be either isothermal or if there is heat transfer, the heating or cooling rates must be low enough to not cause appreciable change in the ratio of the mass-averaged temperature to the surface temperature.

hydrodynamically fully developed flow: A hydrodynamically fully developed flow is identified by four distinct characteristics: (a) the surface shear stress has a constant value; (b) the axial pressure gradient has a constant value; (c) the flow radial velocity (axisymmetric flows) or transverse velocity (planar flows) has a zero value for all cross-stream locations; and (d) the non-dimensional axial velocity profile (the axial velocity profile normalized by the mass-averaged velocity) has a profile of constant, non-changing shape. A requirement for hydrodynamically fully-developed flow is that fluid properties remain approximately constant, which means the flow must be either isothermal or if there is heat transfer, the heating or cooling rates must be low enough to not cause appreciable change in the ratio of the mass-averaged temperature to the surface temperature.

I top of page

ideal gas: In TEXSTAN, this is the calorically imperfect gas model, and it is the variable property model kfluid=2, where the user specifies only the fluid pressure. This model uses the ideal gas equation of state for density, ρ = P/ (RT). For heat transfer, the fluid enthalpy is a only a function of temperature (thermally perfect equation of state), and Prandtl number is also considered a function of temperature. The concepts of ideal gas and perfect gas come from the sciences of thermodynamics and compressible fluid mechanics, and you will find their definitions have some degree of interpretation. This is discussed in depth in perfect gas.

internal flow: TEXSTAN considers only two flow classes: internal (or channel) flows and external flows (currently TEXSTAN does not handle free-shear flows). For both internal and external flows, the boundary layer approximations require specification of the pressure gradient, dP/dx, to mathematically close the set of equations. For the internal flow class the pressure gradient is determined to ensure that the axial (flow-direction) conservation of mass is preserved as the governing equations are solved in the flow direction. Strictly speaking, the pressure gradient at any given axial (x) location should be iterated, but as a first approximation, the pressure gradient in academic TEXSTAN is estimated from the previous (x) location, and a correction is applied without iteration. In TEXSTAN the internal flow geometries include flow in a circular pipe, flow between parallel planes (the flat duct), and flow in an annulus. Note that both the circular pipe and parallel planes duct are limiting cases of the radius ratio that defines the annular geometry.

I-surface: In TEXSTAN, the flow field is contained between the I-surface to the E-surface. For all external flows, the I-surface is the wall (the solid or no-slip surface), and the corresponding E-surface is the free stream. For internal flows, the I-surface location is geometry dependent: for kgeom=4, the I-surface is the pipe or tube centerline and the E-surface is the pipe wall; for kgeom=5, the I-surface is the parallel planes channel centerline (its symmetry line) and the E-surface is the channel wall; for kgeom=6, the I-surface is the (arbitrary) first wall of the parallel planes channel and the E-surface is the second wall; and for kgeom=7, the I-surface is the inner surface of the annulus and the E-surface is the outer surface.

J top of page

K top of page

K acceleration parameter: This parameter is traditionally used in analysis of equilibrium turbulent boundary layers as a measure of the strength of the flow acceleration, and it is formulated as
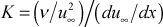
where ν is the fluid kinematic viscosity.

L top of page

large mass transfer: This is an assumption relating to how mass transfer is modeled - see mass transfer.

low speed flow: A low speed flow is typically a flow with a Mach number less than about 0.4. The low speed flow can be calculated with or without considering heat transfer. If heat transfer is being considered, typically the effect of viscous dissipation is not considered unless the fluid is a liquid whose Prandtl number is large (for example viscous oils or any fluid with a Pr > about 5-20), and the viscous dissipation flag is activated by setting jsor(j) =3 for the energy equation. Typically if viscous dissipation is being considered variable properties should also be considered; however, TEXSTAN does not require variable properties for viscous dissipation, and there are several classical analytical solutions in the open literature for viscous dissipation affected constant-property flows.

M top of page

Mach number: The Mach number, M, is used primarily in the variable property solution of gas flows. It is computed within the variable property tables, either by table lookup of the local speed of sound as a function of temperature and then forming the velocity to speed of sound ratio, or it is directly computed if the property is considered an ideal gas.

mass-averaged temperature: The mass-averaged temperature is only used in internal flows. It is also known as the mean temperature, mixed mean temperature, bulk fluid temperature, or mixing-cup temperature. It is the temperature that characterizes the average thermal energy state of the fluid. It derives from the one-dimensional energy equation for an internal flow of a fluid whose static enthalpy model can be defined as the product of its specific heat, c times the temperature, T. The defining equation for the mass-averaged temperature is
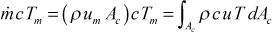
In this equation, ρ is the density, u_m is the mass-averaged velocity, u is the flow axial velocity component, and A_c is the flow cross-sectional area.

mass-averaged velocity: The mass-averaged velocity is only used in internal flows. It is also known as the mean velocity, and it characterizes the average velocity of the fluid. It is a one-dimensional concept, but it does not derive from a momentum balance. The defining equation for the mass-averaged velocity is
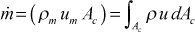
In this equation, ρ is the density, ρ_m is the density evaluated at the mass-averaged temperature, u_m is the mass-averaged velocity, u is the flow axial velocity component, and A_c is the flow cross-sectional area.

mass transfer: The boundary layer mass-transfer equation for an inert substance is based on CHMT Eq. (18-12). The equation is written for laminar flow because the turbulent version has had limited testing within TEXSTAN. The mass transfer equations in TEXSTAN can only calculate small mass transfer of a binary mixture such as water vapor (H₂O) evaporating into an air boundary layer or naphthalene (C₁₀H₈) evaporating into an air boundary layer. Mass transfer is addressed in the section external flows: mass transfer, and the mass transfer boundary layer equation is presented in the overview: transport equations section of this website.

mass transfer coefficient: In TEXSTAN this is the mass transfer conductance, g, and it is the ratio of the surface mass flux to the mass transfer driving force, B - see the external flows: mass transfer section of this website. Note that for a binary mixture with the B much less than unity, the mass transfer driving force reduces to the difference between the surface mass concentration and the free stream concentration of the substance being diffused.

mean temperature: This term is synonymous with mass-averaged temperature.

mean field closure

The concept of mean field closure (MFC) is tied to time-dependent turbulent flowfields, and the idea that for many classes of turbulent flows the velocity field can be decomposed into steady time-independent velocity components and relatively small fluctuating velocity components. This idea is often called the Reynolds decomposition. Note that we ignore periodic flows in this description that would add a periodicity component. When Reynolds decomposition is applied to the Navier-Stokes equations and they are time-averaged (we neglect the issue of density and the need for Favre-averaging), the time-dependence is removed, and as a result there appears a set of six independent double-velocity correlations for the fluctuating velocity components. Likewise, for the energy equation using the same procedure there arises a set of three independent velocity-energy correlations for the fluctuating velocity-fluctuating energy (static enthalpy or temperature) components. These components are labeled six Reynolds stresses and three Reynolds heat fluxes, with or without their accompanying thermophysical properties such as density and specific heat. If we now apply the two-dimensional boundary layer approximations to the time-averaged equations we end up with the traditional boundary layer momentum and energy equations. The momentum equation has a new unknown, the turbulent Reynolds stress, and the energy equation has a new unknown, the turbulent heat flux. We have added two new unknowns to the boundary layer equations because of Reynolds decomposition and time-averaging.

At this point we need to digress to put MFC into perspective. To solve any set of equations we are required to have the number of equations equal the number of unknowns to have a unique solution. In two-dimensional laminar boundary layer flow the fluid stress is an extra unknown, and it is removed by introducing a new "equation", the constitutive equation called Newton's law of viscosity. In this equation (or fluid stress model) the fluid stress is made proportional to the fluid strain rate (which reduces to a velocity gradient when the boundary layer approximations are applied) and the unknown is shifted from being the fluid stress to being the dynamic viscosity. The number of unknowns is removed in theory and replaced by the "known" dynamic viscosity. Thus, the laminar momentum boundary layer problem is "closed" (number of equations equals the number of unknowns). Note, the pressure gradient is technically still be an unknown term, but it is made a known quantity by the Bernoulli equation and the free stream velocity boundary condition via an Euler equation solution or experimental velocity distribution. This is what differentiates boundary layer equations from Navier-Stokes equations - the boundary layer equations always have one more unknown (the pressure gradient) than equations. The end requirement is still the same, the number of equations have to equal the number of unknowns for a unique solution. And this will always be the case for laminar flows being solved by either the boundary layer equations or the Navier-Stokes equations.

We now return to MFC. We assume that the Reynolds shear stress is proportional to the mean field strain rate, and for the boundary layer approximations this reduces to the mean velocity gradient. The constant of proportionality is called the turbulent viscosity, in analogy to the molecular dynamic viscosity. Likewise the Reynolds heat flux is assumed proportional to the mean field temperature gradient, and its constant of proportionality is called the turbulent conductivity in analogy to the molecular thermal conductivity. What is clear is that we have simplified the turbulence problem in one respect, but we have not resolved the closure issue until we adopt a algebraic models for the turbulent viscosity and turbulent conductivity that do NOT introduce any new unknowns. With these algebraic models the turbulent momentum boundary layer problem and turbulent energy boundary layer problem are "closed".

One final observation - the alternative to MFC is Reynolds stress and Reynolds heat flux closure, where transport equations are proposed for the Reynolds stress and Reynolds heat flux. In the end there will always have to be modeling of the unknown terms. To avoid modeling one needs to consider direct numerical simulation or large-eddy simulation (which has only minimal modeling).

mean velocity: This term is synonymous with mass-averaged velocity.

mixed convection

Mixed convective flows are typically low-Re forced convective flows with heat transfer and a gravitational body force component that can be aligned either in the direction of forced flow (aided flow) or against the direction of flow (opposed flow). Mixed flow in TEXSTAN is controlled by the appropriate choice of the momentum equation and energy equation source terms.

Internal mixed convection in channels is a special case, and the solution is overall iterative because the channel exit pressure can not be specified. The user gives TEXSTAN the inlet pressure, the mass flow rate (by way of the initial velocity profile), and the channel length. The flow is computed to the channel exit, and the fluid exit pressure is compared to the expected value (for example, ambient pressure). If the exit pressure is incorrect for the given fluid inlet pressure and channel length, the inlet velocity profile (usually a flat profile) is adjusted and the solution is repeated until the exit pressure from TEXSTAN matches the required exit pressure. Note that some mixed convective flows result in a reverse flow at the exit. This is not a possible solution in TEXSTAN.

mixed-mean temperature: This term is synonymous with the mass-averaged temperature.

mixing-cup temperature: This term is synonymous with the mass-averaged temperature.

momentum thickness: The momentum thickness for planar flow is evaluated from the integral
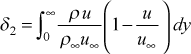
It is the natural variable that arises when the boundary layer momentum equation is partially integrated in the cross-stream direction to form an integro-differential equation called the momentum integral equation, and it's streamwise derivative is seen to be directly proportional to the nondimensional surface shear stress (just as the enthalpy thickness streamwise derivative is directly proportional to the nondimensional surface heat transfer coefficient). In the early days of turbine blade, airfoil, and spacecraft design, solution to the momentum integral equation (and its energy integral equation counterpart) provided momentum and heat transfer solutions. These equations are addressed in depth in our textbook, CHMT. Corrections to this integral for transverse curvature is described in the external flows: Reynolds number section of this website.

N top of page

numerical accuracy: Numerical accuracy is rooted in the integration stepsize and how the grid is constructed, and this is described in the overview: numerical accuracy section of the website.

numerical grid: The numerical grid - or finite difference mesh - is created using the initial velocity profile, u(y), and the same distribution of y locations is used for the other dependent variables. The details of establishing the mesh is described in the overview: numerical accuracy section of the website.

numerical method: TEXSTAN has a hybrid implicit-explicit numerical scheme that is described in the Numerical Solution Procedure part of the overview: transport equations section of this website.

Nusselt number: The Nusselt number for heat transfer, Nu, represents the heat transfer coefficient that is nondimensionalized using conduction transport variables - see the external flows: heat transfer and internal flows: heat transfer sections of this website.

O top of page

P–Q top of page

perfect gas

In TEXSTAN, this is the calorically perfect gas model, and it is the variable property model kfluid=14, where the user specifies the fluid pressure, the fluid molecular weight, the fluid ratio of specific heats, and the fluid Prandtl number. The perfect gas model uses the ideal gas equation of state for density, ρ = P/ (RT), the fluid enthalpy is a function of temperature, but it is computed from a constant specific heat, and Prandtl number is also held constant.

The concepts of perfect gas and ideal gas come from the sciences of thermodynamics and compressible fluid mechanics, and you will find their definitions have some degree of interpretation. For background, a gas is considered a single-phase substance (non-reacting), requiring a single reversible work transfer mode (dw=Pdv) and a single reversible heat transfer mode (dq=Tds, from the second law of thermodynamics). Thus there will be a requirement for a single mechanical equation of state and a single thermal equation of state. All thermodynamic functions that describe the state of the fluid (gas) must be functions of two independent state variables (because of one work mode and one heat transfer mode). For the single-phase gas, these variables can be the pressure, P, and the temperature T. Thus, the specific volume (inverse is density), specific internal energy, and specific enthalpy become functions of (P,T).

The mechanical equation of state for a perfect gas comes from consideration of Boyle's Law and Charles' Law, leading to the density (inverse specific volume) calculated using ρ = P/(RT), and R is the molecular-specific gas constant for the gas (equal to the universal gas constant divided by the molecular weight of the gas). This equation is also called the ideal gas equation of state - they are the same. We see that ρ = ρ(P,T). For real gas behavior, the equation can be altered, and a simple model is to include a compressibility factor, Z, and ρ = ρ(Z,P,T).

The thermal equation of state for a perfect gas comes from combining the ideal gas equation of state with the first law of thermodynamics for a single-phase substance and the definitions of the specific heat functions. Because of the ideal gas (perfect gas) equation of state, the thermodynamic properties internal energy and enthalpy become only a function of temperature, specified in terms of specific heats, de = c_v dT and di = c_p dT. Note that both specific heats retain their function of temperature, c_v=c_v(T) and c_p=c_p(T), and their ratio, γ=(c_p /c_v) is also a function of temperature. This is the thermally perfect equation of state for a gas. Because this form of the model retains temperature dependencies for the specific heats, it is sometimes called the calorically imperfect gas model. In TEXSTAN a fluid that obeys the calorically imperfect model is called an ideal gas. Note that the ideal gas model retains the Prandtl number temperature dependency.

A calorically perfect gas model is the thermally perfect equation of state whose specific heats are held constant (calorically perfect). The ideal gas equation of state for density is retained, and the Prandtl number is a fixed value and not permitted to vary with temperature.

Prandtl number: The Prandtl number, Pr, is an important dimensionless quantity relating thermal transport to momentum transport. It is comprised of thermophysical properties, Pr = μ / (k/c), and it can be reconstructed to be the ratio of the momentum diffusivity to thermal diffusivity. In convective heat transfer it is used in correlation of the heat transfer data and in correlation of the ratio of the thermal and momentum boundary layer thicknesses.

pressure

The TEXSTAN input variable for pressure is po.

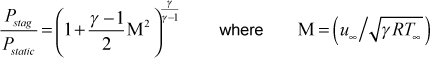
For external flows that are variable property gas flows po is considered the stagnation pressure, P^* or P_stag , and it is the sum of the fluid static pressure and a kinetic pressure term. The corresponding free stream static pressure is initialized at the location xstart by first computing the Mach number at that location and then using the 1-dimensional perfect gas formulation ratio Ptotal/Pstatic

where γ is the ratio of specific heats. The γ variable is either an input variable gam/cp for the kfluid=14,15 perfect-gas model or it is an entry in variable property tables for the other gas model options.

For external flows that are constant property gas flows and for all constant or variable property liquid flows over external geometries, po is assumed to be the free stream static pressure at xstart. Because of the boundary layer assumptions and the assumption of no effect of curvature on pressure, the fluid static pressure will be constant over the external flows.

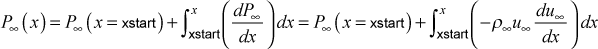
For external flows with variable free stream velocity the free stream static pressure is changed during integration using the Bernoulli equation, static P integral external flow

For internal flows the input variable po is assumed to be the static pressure at xstart, and the pressure is assumed to be constant over the flow cross section.

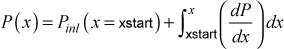
For internal flows the pressure is changed in the flow direction by first establishing the local pressure gradient at each x location using an iterative scheme to satisfy the axial flow direction conservation of mass at that location, and then integrating in a manner similar to how the external pressure gradient is integrated, static P integral internal flow

pressure gradient

For external flows the pressure gradient is specified via the streamwise-direction distribution of the free stream velocity distribution u_∞ (x). The local pressure gradient is then calculated using Euler's streamline-direction equation for inviscid fluid motion, ignoring axial-direction surface curvature:

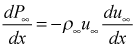
For internal flows, the pressure is changed during integration by first establishing the local pressure gradient at each x location using an iterative scheme to satisfy the axial flow direction conservation of mass at that location.

R top of page

recovery factor: The recovery factor, r_c , is described in the calculation procedure for the adiabatic wall temperature.

recovery temperature: This term is synonymous with the adiabatic wall temperature.

Reynolds analogy

The Reynolds analogy can be applied to both laminar and turbulent flows. For laminar flows, the root of the analogy is in the similarity of the nondimensional profiles for velocity, temperature, and mass concentration, leading to the nondimensional surface quantities being equal, as described by the friction coefficient divided by two equal to the heat transfer Stanton number equal to the mass transfer Stanton number, c_f /2 = St = St_m. This similarity will occur under the following restrictions: the free stream velocity is constant, the surface temperature is constant, and the surface mass concentration for m_j in a binary mixture is constant, along with constant properties and no viscous dissipation. The nondimensional fluid transport parameters Prandtl number and Schmidt number must also be unity, Pr = Sc = 1.00, where Pr is the ratio of the momentum diffusivity, ν, to thermal (heat) diffusivity, α, and Sc is the ratio of the momentum diffusivity to the mass transfer diffusivity, D_j. This equality of diffusivities is the Reynolds analogy, and it leads to the similarity of the nondimensional profiles because with the analogy the mathematical form of the governing differential equations and boundary conditions are similar. From an engineering perspective, the analogy permits interchange of momentum, heat, and mass transfer results. The classical extension of this analogy permits incorporation of the effects of near unity Pr and Sc, and sometimes called the Chilton-Colburn analogy or j-factor analogy in the chemical engineering and heat exchanger literature where c_f /2 = St Pr^2/3 = St_m Sc^2/3 and the latter two quantities are called j_H and j_M.

For heat and mass transfer studies, the Lewis number is defined as Le = Pr/Sc, and Le = 1.00 permits heat transfer experimental investigations to be completely interchangeable with mass transfer experimental investigations, providing the restrictions mentioned above are applied. Corrections for near-unity Le experiments are often applied to the experimental data.

For turbulent flow, modeling turbulent transport using mean field closure introduces the turbulent diffusivity for momentum, ε_M , and the corresponding turbulent diffusivity for heat, ε_H . The laminar Reynolds analogy is extended by forming the turbulent Prandtl number, Pr_t equal to the ratio of these two turbulent diffusivities, and Pr_t = 1.00 is the turbulent Reynolds analogy. As with laminar flow, when this analogy holds the nondimensional turbulent velocity and temperature profiles are expected to be similar, leading to c_f /2 = St. The idea of Pr_t = 1.00 implies the distribution of turbulent shear stress and turbulent heat flux are equal throughout the flow. This has been studied in depth for purposes of turbulent transport modeling and development of models for Pr_t.

S top of page

Schmidt number: The Schmidt number, Sc, is an important dimensionless quantity relating mass transport to momentum transport. It is comprised of thermophysical properties, Sc_j = (μ/γ_j ), and it can be reconstructed to be the ratio of the momentum diffusivity to the mass diffusivity of the j-th species. In convective mass transfer it is used in correlation of the mass transfer data and in correlation of the ratio of the mass transfer and momentum boundary layer thicknesses.

separation: For external flows, separation is generally caused by either a significant momentum flux into the boundary layer by blowing, from either a large or a prolonged adverse pressure gradient in forced convection flows, or from body forces in opposition to the x-directed momentum flow in free convection flows. When the flow separates, the surface shear stress goes to zero, and the streamlines move away from the surface. In TEXSTAN, the input variable fra was designed to try to more accurately predict the separation point by reducing the integration stepsize. Because of the numerical formulation within TEXSTAN, computation of separated flow is not permitted, and TEXSTAN stops, often to the frustration of the user because of how different computers and compilers handle divide by zero which is the consequence of flow separation.

shape factor: The shape factor is the ratio of the displacement thickness to the momentum thickness,
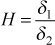
and it has been used in classical aerodynamics as a predictor of whether the momentum boundary layer is laminar, or transitional, or fully turbulent. Because it contains the displacement thickness, which is subject to strong variable property influence, the shape factor is primarily useful for incompressible flow.

small mass transfer: This is an assumption relating to how mass transfer is modeled - see mass transfer.

stagnation pressure: See pressure.

stagnation temperature: See temperature.

Stanton number: The Stanton number for heat transfer, St, represents the heat transfer coefficient that is nondimensionalized using convection transport variables - see the external flows: heat transfer and internal flows: heat transfer sections of this website. The Stanton number for mass transfer, St_m, represents the mass transfer conductance that is nondimensionalized using convection transport variables - see the external flows: mass transfer section of this website.

static pressure: See pressure.

static temperature: See temperature.

suction: For external flows, suction is the removal of low-momentum transfer of fluid through a surface and from the boundary layer. Adverse pressure gradients tend to cause the streamlines to move away from a surface, leading to flow separation, and suction can be used as a means to keep the streamlines attached. Suction is described in more depth in the glossary entry transpiration.

T top of page

temperature

For external flows, the TEXSTAN input variable for temperature is tstag, and for internal flows there are two input variables, tref and wall.

For external flows that are variable property gas flows tstag is considered the stagnation temperature, T^* or T_stag , and it is the sum of the fluid static temperature and a kinetic energy term. The free stream static temperature at xstart is initialized by interpolating the ubI(m) array to determine the free stream velocity at this location and then calculating the static temperature by removing the kinetic energy term. At each axial location the free stream temperature is computed based on the local free stream velocity.

For all constant property external flows, tstag is assumed to be the free stream static temperature at xstart, and it is not permitted to vary in the flow direction.

For all internal flows the input variable tref is considered a static temperature, T_ref , and it is used in conjunction with the input variable twall to construct an initial or entry temperature profile, and then converted to a stagnation enthalpy profile if variable properties are being considered.

The fluid temperature, T, is a static temperature by definition, and it is often called the thermodynamic temperature of the fluid. This is the temperature used for all fluid property calculations. If the fluid properties are constant (kfluid=1), TEXSTAN interprets the energy equation as a temperature equation, and all temperatures are considered static temperatures. If the fluid properties are variable (kfluid>1), TEXSTAN interprets the energy equation as a stagnation enthalpy equation, and when a stagnation enthalpy profile is computed at each integration step, it is converted into a static temperature profile using variable property equations or tables to determine the thermophysical properties at each cross-stream y location.

thermal entry length: The thermal entry length in channel flow is the distance from the start of application of the thermal boundary condition to the point where the flow becomes thermally fully developed. Typically the entry length is defined when the nondimensional temperature profile becomes independent of x to within a certain percent, typically to within five percent or smaller.

thermally fully developed flow: A thermally fully developed flow is primarily identified by examining the nondimensional temperature profile, constructed as the ratio
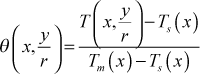
where T_m is the mass-averaged temperature and T_s is the surface temperature, both functions of the axial flow direction. The double variables y and r indicate the definition can be for either a planar or an axisymmetric flow. The test for thermally fully developed flow is when this nondimensional temperature profile becomes independent of x. A requirement for thermally fully-developed flow is that fluid properties remain approximately constant, which means the flow must be either isothermal or if there is heat transfer, the heating or cooling rates must be low enough to not cause appreciable change in the ratio of the mass-averaged temperature to the surface temperature. Note that the flow must become hydrodynamically fully-developed before the flow can become thermally fully developed.

total pressure: This term is synonymous with stagnation pressure - see pressure.

total temperature: This term is synonymous with stagnation temperature - see temperature.

transpiration: When fluid is either added or removed from the surface of a bound flow (external geometry or internal geometry), surface heat transfer (heat flux) and momentum transfer (friction) can be significantly changed. There are two primary mechanisms for this fluid addition or removal. The first is to have a phase change occurring at the surface, for example evaporation or condensation) and the second is to have the surface be micro-porous and a fluid be either injected (blowing) or removed (suction) through the surface. The porous surface mechanism is called transpiration in boundary layer theory. If the injection is through discrete holes in the surface it is called discrete-hole film cooling. What distinguishes transpiration is the surface mass flux is quite small compared to the cross-flow mass flux. The definition is related to the blowing fraction: F = (ρv)_s / (ρv)_∞ . For blowing the limit is typically F=0.01, and for larger values the flow separates from the surface. A small value of blowing (+F) can significantly reduce friction and heat transfer, and a corresponding small amount of suction (-F) can have the opposite effect. For laminar flows, blowing and suction are a part of the Falkner-Skan flow family of analytical solutions, and TEXSTAN can calculate these flows.

turbulence intensity: The turbulence intensity, Tu, is the ratio of the square root of the turbulence kinetic energy to a reference velocity. See the Boundary Conditions part of modeling: two-equation model section of this website or the input variable tuapp.

turbulent Prandtl number: The turbulent Prandtl number, Pr_t, is defined by analogy to the laminar Prandtl number as
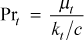
and it is presented in the overview: transport equations and modeling: turbulent Prandtl number sections of this website.

U top of page

unheated starting length flow: An unheated starting length flow is an internal flow that has an adiabatic section at the beginning of the channel, and the channel length is sufficiently long to permit the flow velocity profile to become hydrodynamically fully developed before the thermal boundary condition is changed to cause fluid heating or cooling. A requirement for hydrodynamically fully-developed flow is that fluid properties remain approximately constant. The unheated starting length then becomes the distance from the channel entrance to the start of heating or cooling.

V top of page

variable properties: For external flows the use of variable properties (kfluid > 1) is required for gases when the ratio of surface temperature to free stream static temperature for cooling is (T_s / T_∞) < 0.90 and for heating when (T_s / T_∞) > 1.10. For liquids the range reduces to (T_s / T_∞) < 0.95 or (T_s / T_∞) > 1.05. For internal flows the free stream temperature is replaced by the mass-averaged (mean) temperature, T_m , and the same general rules apply. Cooling is defined as removal of energy from the flow, and heating is defined as energy addition to the flow. Note that Mach number flows that are transonic and higher (Ma > 0.85) will induce significant variable property effects due to the conversion of work to heat in the near-wall region, called viscous dissipation, and variable properties are required.

viscous dissipation

For external flows viscous dissipation in gases begins to become important when the Mach number, Ma, exceeds 0.4, and it becomes extremely important for Mach numbers that are transonic or higher, Ma > 0.85. For liquids it is also important for high subsonic flows. For internal flows, viscous dissipation in gases and liquids is important for high-subsonic flows, and it is especially important for low-speed flow of liquids in which the Prandtl number is large (typically Pr > 5-20).

To properly model high speed flows the energy equation must be solved to capture the effect of variable properties caused by viscous dissipation (viscous work effect). The variable properties flag kfluid is set > 1 (appropriate to the fluid of choice) and the viscous dissipation flag is activated by setting jsor(j) =3 for the energy equation. For low-speed flows of high Pr fluids, variable properties are not required to consider viscous dissipation.

Viscous dissipation has its roots in the thermal energy equation, a First Law of Thermodynamics equation that represents how the combined rates of work transfer and heat transfer affect the convective transport of the fluid's specific internal energy, specific kinetic energy, and specific potential energy. The rate of work transfer relates to the total stress tensor and to how surrounding fluid elements do work based on the three components that make up the total stress tensor: viscous shear stresses, rotational shear stresses, and normal stresses.

We assign a shear-shaft work label to the viscous rotational shear stress component of work rate (often it arises from a shaft work input), we assign a viscous work label to the viscous shear component of work rate, and we assign the flow work label to the normal stress (or) compressive component of work rate. We then keep the shear-shaft work rate term and the heat transfer rate term on the left hand side of the First Law equation (the classic work and heat terms), and we move the other two work rate terms to the right hand side of the equation.

If we wish to call the First Law equation a stagnation enthalpy equation, we combine the flow-work rate term of the normal stresses (fluid displacement of fluid) with the convective transport of the fluid specific internal energy and specific kinetic energy and call this term collectively the convective transport of the stagnation enthalpy of the fluid. We neglect the specific potential energy of the fluid. The last term on the right hand side of the stagnation enthalpy equation is the viscous work rate term. On a differential basis it is the product of the velocity vector and the shear components of the viscous stress tensor.

A traditional form of the energy equation applicable to low-speed constant-property flows is the so-called split energy equation, and in its reduced form the temperature equation. Consider the boundary layer formulation (for ease of description) of the momentum equation and stagnation enthalpy equation. Take the momentum equation and multiply it by the flow-direction u velocity component to create a mechanical energy boundary layer equation and subtract this equation from the stagnation enthalpy equation. In doing so, we remove mechanical energy from the First-Law formulation and we are left only with what we call the split energy equation (sometimes called the static enthalpy or internal energy equation). This equation removes the thermodynamically reversible component of the viscous work term and what remains is the irreversible component - which is the viscous dissipation that represents conversion of mechanical work to thermal energy. The split energy equation is equally correct as an energy equation and it is required when formulating combustion mass transfer problems.

In summary, TEXSTAN is formulated with the exact First-Law based stagnation enthalpy equation as the energy equation. TEXSTAN does not use the split energy equation primarily because it only does limited mass transfer problems. For constant properties, the stagnation enthalpy equation reduces to a temperature equation by assuming a fluid model that approximates the fluid as either an ideal gas or as an incompressible liquid (without the flow-work term). This form of the temperature equation has the viscous work term reformulated as a viscous dissipation term (precisely the same as what one finds in most undergraduate heat transfer texts).