numerical accuracy

• Integration Stepsize
• Grid or Finite Difference Mesh

Of primary importance in using numerical codes to solve engineering problems is the understanding of how to achieve numerically accurate calculations. This idea is partly addressed in the section home: YOU - the user of this website. As TEXSTAN was developed (and its predecessor STAN5), every effort was made to ensure it could accurately reproduce classical benchmark boundary-layer flows and internal flows, both laminar and turbulent. This is primarily why the benchmark datasets were created. These datasets contain special output (using kout=8) that reproduce ratios of TEXSTAN-computed friction and heat transfer results to values computed from widely accepted correlations. For example, the Blasius boundary layer solution or thermally fully-developed pipe flow solution are two important benchmarks. Turbulent boundary layer and pipe/channel benchmark datasets are also evaluated using each of the choices of turbulence models described in the modeling section. From evaluation of these benchmark datasets have come an understanding of how to achieve numerically accurate calculations, and these numerical experiments are the basis for our recommendations for parameters that control grid construction and stepsize.

Numerical accuracy is rooted in the integration stepsize and how the grid is constructed. TEXSTAN has a hybrid implicit-explicit numerical scheme (as described in the overview: transport equations section). The finite difference (or finite volume) formulation is numerically implicit in the cross-flow direction and numerically explicit in the flow direction. The implicit nature of the formulation would normally permit numerically accurate results without too much attention to the distribution of points (subvolumes) in the cross-flow direction, but TEXSTAN's transformed grid represents mass flow (a nondimensional stream function) so point distribution remains important, especially for resolving turbulent heat transfer. The explicit nature of the formulation requires careful attention to the integration stepsize.

Integration Stepsize - This is controlled in the flow direction primarily by the deltax variable, which is a nondimensional quantity, that for external flows is the fraction of velocity boundary layer 99% thickness and for internal flows is a fraction of the pipe radius, or channel half width, or average annulus radius.

For external flows, the numerical grid extends only from the surface to just above the shear layer (boundary layer). This is usually called the free stream or edge. For external flows TEXSTAN's integration stepsize is proportional to the boundary layer thickness, so as the boundary layer grows, the stepsize automatically increases. The primary input variable for stepsize control is deltax. We typically set deltax =0.05 to =0.10, and this works well for most laminar, transitional, and turbulent flows. However, the integration stepsize must be kept smaller to resolve fast-changing boundary conditions. In the event the boundary layer grows too fast in an attempt to entrain free stream energy to overcome separation (adverse pressure gradients), there is a control variable fra to further limit the stepsize, by not permitting the boundary layer to grow more than a certain percentage (in terms of overall mass flow rate per unit width) with each integration step.

For internal flows, the numerical grid is required to extend from the surface to the centerline for pipes and thermally-symmetrical parallel-planes channels (kgeom=4,5) or from surface to surface for thermally-asymmetrical parallel-planes channels and annuli (kgeom=6,7). As with external flows, we typically set deltax =0.05 to =0.10, and this works well for pipe and channel flows once the developing shear layer (boundary layer) diffuses to the pipe or channel centerline. However, the integration stepsize must be kept much smaller to resolve the entry flow where the shear layer starts with zero thickness.

The combined entry flow in pipes and channels begin with flat profiles for velocity and temperature, so the developing shear layer (boundary layer) is a really a very small percentage of this grid in the beginning. If deltax is set small enough to resolve the extremely high wall gradients in the beginning part of the entry region, the total number of integration steps will be massively large by the time the entry flow is complete and fully-developed flow begins. Instead of using deltax we set the flag kdx =1, set deltax =0, and input deltax information using the array aux1(m) which is then linearly interpolated as a function of x . This is why the user will see a peculiar x(m) distribution, and the small aux1(m) values near x=0. The actual integration stepsize becomes proportional to the interpolated aux1(m) array, =aux1*yl , where yl is the pipe radius, half-width of a parallel-planes channel, or the average of the inner and outer radii for an annulus.

The details of controlling integration stepsize for external flows is discussed in detail in the external flows: integration control section of this website and the corresponding details for internal flows is discussed in detail in the internal flows: integration control section of this website.

Grid or Finite Difference Mesh - The distribution of grid points is established by the initial velocity profile, u(y). To see this, we first recall that the y coordinate is transformed such that u(y) becomes u(ψ) using the von Mises transformation in its inverted form

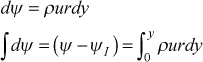
The u(ψ) is then converted to u(ω) using the definition
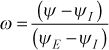
where Ψ_I is arbitrarily set equal to zero, and Ψ_E is the upper limit of the integral of the inverted von Mises integral of u(y). Details of these transformations are explained in detail in the generalized transport equation part of overview: transport equations section.

From this equation we see the cross stream variable ω represents the percentage of mass flow rate per unit span (or per unit radian) referenced to the I surface and Δω = Δψ represents the mass flow per unit span (or per unit radian) in a stream tube measured between any two grid (finite difference) locations. Again, for planar surfaces we set r=1 in the transformation.

Experience has shown that changes in y should be small to achieve grid independence for the nondimensional stream function coordinate system. Therefore, we recommend (and use) the classic compound-interest formulation for the y-distribution in the near-wall region of the shear flow and once it has expanded (away from the wall) to a certain percentage of the overall shear layer thickness (boundary layer thickness or channel half-height), it is fixed constant.

The recommended grid construction is as follows. The first y location in the grid is y(1)=0, and the second y location is calculated to be y(2)=del99*dyi, where del99 for pipe flows will be the wall radius, for parallel-plane channel flows it will be the channel half height, for annular flows it is arbitrarily set equal to the average of the inner and outer radius, and for boundary layers it is the 99% boundary layer thickness. The next location is power-law expanded (sometimes referred to as a compound interest formulation) to be y(3)=y(2)*(1+rate), and so forth. The expansion is permitted to continue until the value of y exceeds (0.035-0.05)*del99, and from that location outward, all y values are equally spaced at (0.035-0.05)*del99. This algorithm is used for both planar and axisymmetric coordinates, and then for the axisymmetric r coordinate in pipe flow y is linearly transformed such that r=0 becomes the centerline, and for the annulus, it is the inner wall radius. With this overall algorithm, there will be a significant number of points near the no-slip surface, depending on the values of both variables. For laminar flow, the suggested variables have been proven to provide grid-independent solutions over the laminar Re range. For turbulent flow, the grid will be much finer to insure that once the flow becomes fully turbulent, there will be a significant number of points within the laminar sublayer (y⁺ < 10 for smooth wall turbulent flows). Again the recommended values for dyi and rate have been tested for grid independent friction and heat transfer results.

In summary, the compound-interest based spacing grid yields a transformed grid that provides numerically grid-independent solutions providing the user follows the suggested guidelines for the dyi and rate variables associated with the initial profile construction. These guidelines have been carefully established by testing using the various benchmark datasets.