turbulent Prandtl number

TEXSTAN uses the Kays turbulent Prandtl number model, developed in detail in our textbook CHMT. The model evolved from a simple conduction model for Pr_t that includes heat conduction to or from the turbulent element (eddy) as it moves. The following equation fits the available experimental data reasonably well
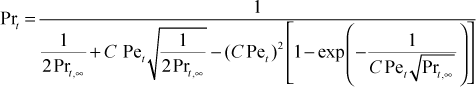
where Pe_t = (ε_M/ν) Pr is a turbulent Péclet number. C is an experimental constant equal to 0.3. The far-field value of the turbulent Prandtl number, Pr_t,∞ , is set equal to 0.86 for gases and light liquids, and for Pr< 0.6 (liquid metals), the Weigand correction is applied

The Pr_t model has been calibrated for equilibrium turbulent boundary layers for use with the mixing-length turbulence model. It works equally well for turbulent flows with one- and 2-equation turbulence models. This option is not recommended for transitional boundary layer flows or flows with pressure gradients, or for liquids with Pr > 10-20.

Note, for turbulent mass transfer, the turbulent mass flux would be specified through a turbulent Schmidt number. However, there is currently no provision in TEXSTAN to input a turbulent Schmidt number.

The flag ktme identifies the turbulent Prandtl number model choices for computing the turbulent conductivity.

ktme	turbulence model for the energy equation
= 1	constant turbulent Prandtl number; =0.85
= 2	constant turbulent Prandtl number, = fxx
= 3	Kays variable turbulent Prandtl number model