transport equations

The transport equations are often called boundary layer equations, in reference to the boundary layer approximations that are valid for a large class of flows whose streamlines move principally in one direction. The equations apply equally to flow over external surfaces and to flow within pipes, channels, and ducts. The mathematical requirement for the equations is that they are formulated as parabolic equations, solved in TEXSTAN by a classical numerical marching technique in a two-dimensional (2-D) solution domain from the starting boundary of the domain to the end boundary. The boundary conditions are such that they can never cause the flow streamlines within the domain separate or to turn back on themselves. The equations are formulated for an axisymmetric coordinate system that uses y as the cross-stream variable. This is permitted for axisymmetric flows because there is a well-defined relationship between the cross-stream variable r and the cross-stream variable y. For example, in pipe flow, y = (r_s - r) and y is measured from the no-slip surface. Note that the variable r is retained wherever it is required to reflect a differential radial area. With this formulation, when r is set to unity, the Cartesian form of the equations are recovered from the axisymmetric equations. The equations are adapted from our textbook CHMT. Three of the equations are developed in detail to help demonstrate the similarities between the axisymmetric and planar forms and how straightforward they can be changed between the two coordinate systems.

The equations are formulated for turbulent flow, with the turbulence models formulated using mean field closure and described in detail in the modeling section of this website. With this formulation, when the turbulent component of the transport coefficient (for example turbulent viscosity or turbulent conductivity) is set to zero, the laminar form of the equations are recovered. In presenting the equations we have chosen not to adopt the conventional symbols for denoting turbulent flow that show mean quantities with the conventional Reynolds-decomposition time-averaging "bar" symbol over the variable. This choice is primarily because the same equations are being used for both laminar and turbulent flows.

• Flow and Calculation Domains
• Conservation of Mass
• Momentum Equation
• Stagnation Enthalpy Equation
• Temperature Equation
• Mass Transfer Equation
• Generalized Transport Equation
• Numerical Solution Procedure

Flow and Calculation Domains - TEXSTAN solves two-dimensional flows in either Cartesian coordinates for planar flows or axisymmetric coordinates for axisymmetric flows. The variable x is used to denote the flow direction, and this coordinate is sometimes referred to as an intrinsic coordinate or a streamline coordinate. The variable y is used as the as the cross-stream variable, which is permitted for axisymmetric flows because there is a well-defined relationship between the cross-stream variable r and the cross-stream variable y.

The flow domain is defined by its axial extent and its cross-flow extent. For example, for flow over a flat plate the axial extent could be from the plate leading edge to the trailing edge, and the cross-flow extent from the no-slip surface to the free stream. Likewise, for flow in a pipe, the axial extent could be from the entrance to exit, and the cross-flow extent is from the pipe centerline to the no-slip surface. For a turbine blade the flow domain would begin upstream of the leading edge and extend past the trailing edge, and for a nozzle it would be from upstream of the contraction to the expansion area past the nozzle throat. The flow domain is purely conceptual in that it contains the surface(s) for which the shear flow will be resolved.

The computational domain is defined by its axial computational extent and its cross-flow computational extent. The computational domain resides within the flow domain. This is the domain over which the transport equations are solved by TEXSTAN to resolve the flow profiles and surface properties such as wall shear stress and wall temperature (for the Neumann problem) or wall heat flux (for the Dirichlet problem).

The cross-stream computational domain is always identical to that of the flow domain. The bounds of the domain are renamed the I-surface and the E-surface. For external flows the no-slip surface is called the I-surface, and the free stream is called the E-surface. For internal flows that are either pipe flows or thermally symmetrical flows in planar ducts, the centerline is called the I-surface and the no-slip surface is called the E-surface. For thermally asymmetrical flows in planar ducts and for the flows in an annulus, the I- and E-surfaces are the inner and outer no-slip surfaces respectively.

The axial computational domain is bound between the starting location for integration, x = xstart and the location where the user wants the integration to stop, x = xend. Typical starting x locations would be close to the leading edge of a flat plate for the Blasius problem, or it can be exactly at the entrance for a pipe-flow problem. It can not be at x=0 for any flow that has a zero velocity at that point, relating to the nature of the von Mises transformation of the TEXSTAN equations.

Conservation of Mass - The conservation of mass is derived using a differential control volume and assuming two-dimensional axisymmetric flow
where x is the flow-direction variable and y denotes the cross-stream variable. The differential areas for the flow in the flow and cross-steam directions are
and r is the transverse radius of curvature for axisymmetric geometry. For Cartesian geometry, r can be considered unity, and the 2π term divides out. Substitution for the differential area terms and division by 2πdxdy leads to the boundary layer conservation of mass equation, applicable to either laminar or turbulent flow
Note, if the flow is highly compressible or hypersonic, the classical time-averaging is often replaced by Favre-averaging ideas that include density fluctuations.

Momentum Equation - To derive the boundary layer momentum equation for turbulent flow, we create an x-boundary layer energy balance in terms of x-convection (flow direction) and y-convection (cross-stream direction) of x-momentum, a total stress term comprised of viscous and turbulent terms, a pressure gradient term, and a generalized body force
where dV is the differential volume over which the body forces per unit volume act,

Substitution for the mass flow rate terms, differential area terms, and division by 2πdxdy leads to the conservative form of the momentum equation

The total stress is composed of the molecular term and the Reynolds stress term
and modeled using mean field closure as a combination of the molecular and turbulent viscosity to create an effective viscosity

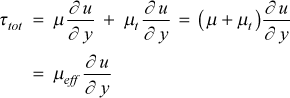
The effective dynamic viscosity (μ_eff) is seen to be the linear combination of the molecular dynamic viscosity (μ) and the turbulent dynamic viscosity (μ_t).

In laminar flow the dynamic viscosity (μ) is often replaced by the kinematic viscosity (ν=μ/ρ), and the terminology kinematic viscosity and diffusivity for momentum are identical and interchangeable. Within TEXSTAN the turbulent viscosity (μ_t) is often replaced by the interchangeable terms turbulent diffusivity for momentum (ν_t =μ_t /ρ) and eddy diffusivity for momentum (ε_M =μ_t /ρ). Thus, the effective viscosity can be formulated two ways.

Combining the conservative form of the momentum equation with the conservation of mass and applying the definition of the total stress yields the final form of the boundary layer momentum equation in TEXSTAN

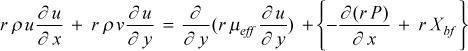
Stagnation Enthalpy Equation - To derive the boundary layer stagnation enthalpy equation for turbulent flow, we start with the x-boundary layer energy balance in terms of x- and y-convection of stagnation enthalpy, a total work comprised of viscous and turbulent work, and a total heat flux representing molecular and turbulent heat transfer in the y-direction, work against the generalized body force term, and a generalized energy source
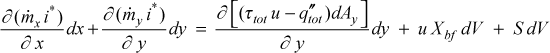
where i^* is the stagnation enthalpy, defined using the boundary layer approximations as the sum of the internal energy, e, and the streamwise kinetic energy per unit mass,

Substitution of the mass flow rate terms, differential area terms, division by 2πdxdy, and combining with the conservation of mass leads to

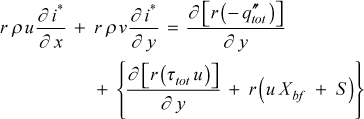
The total heat flux is modeled using the gradient of the static enthalpy, i, which assumes for the molecular heat flux a thermodynamic model of either i(T), or i(P,T) coupled with a weak dependence on P(y), to create an effective thermal conductivity

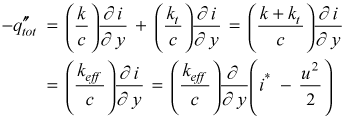
The effective thermal conductivity (k_eff) is seen to be the linear combination of the molecular thermal conductivity (k) and the turbulent thermal conductivity (k_t), with the sign convention following Fourier's law.

In laminar flow the thermal conductivity (k) is often replaced by the laminar diffusivity for heat (α = k/ρc), and using this analogy the turbulent conductivity (k_t) is often replaced by the eddy diffusivity for heat (ε_H = k_t /ρc). Thus, the effective thermal conductivity can be formulated two ways.

Substitution into the stagnation enthalpy equation yields

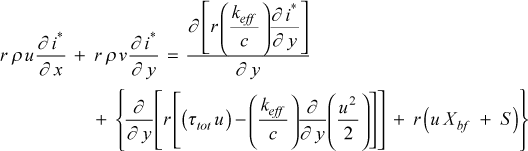
The effective Prandtl number is defined as
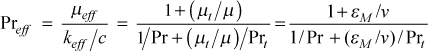
where the laminar Prandtl number is Pr = μ /(k/c) and the turbulent Prandtl number is defined by analogy as

From an experimental point of view, the turbulent Prandtl number for mean field closure can be determined by measuring the turbulent shear stress and turbulent heat flux along with the mean field gradients of velocity and temperature.

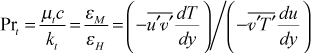
The final form of the boundary layer stagnation enthalpy equation becomes

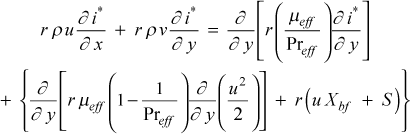
Note, this stagnation enthalpy equation can easily be converted to a temperature equation by replacing the stagnation enthalpy symbol by the temperature symbol, and dividing by specific heat.

Temperature Equation - The boundary layer temperature equation is based on the stagnation enthalpy equation, neglecting the velocity-pressure gradient term, body force work, and volumetric energy source term. This equation is

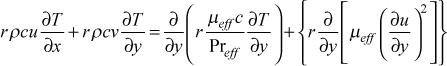
Mass Transfer Equation - The boundary layer mass-transfer equation for an inert substance is based on CHMT Eq. (18-12). The equation is written for laminar flow because the turbulent version has had limited testing within TEXSTAN.
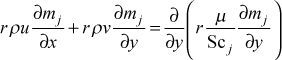
where the dependent variable is the mass fraction (or concentration) m_j = (ρ_j /ρ_mix) in units of kg(j)/kg(mix) or lbm(j)/lbm(mix). In this equation the diffusion coefficient term has been redefined using the Schmidt number equivalent of the Prandtl number for heat transfer, (γ_j = μ/Sc_j). A typical example of m_j would be water vapor in an air-water vapor boundary layer or naphthalene in an air-naphthalene boundary layer.

Generalized Transport Equation - If we examine these various boundary layer equations we observe that they all conform to a common or generalized form: convective transport of a dependent variable φ is balanced by the diffusive transport (laminar + turbulent) of φ and the sources and/or sinks (positive and negative sources) for the generation or destruction of φ while it is in transport.

In this generalized form the momentum equation dependent variable would be φ = u; for the stagnation enthalpy equation, φ = i^*; for the temperature equation, φ = T; and for the mass-transfer equation for an inert substance, φ = m_j. Again, we remind the reader that these equations are in their nonconservative form. Otherwise, for example, the momentum dependent variable would be (ρu), and so forth.

In the strictest sense TEXSTAN is a parabolic partial differential equation solver for equations of the this generalized or common form
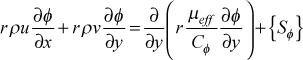
where C_φ equals unity for momentum, and for the various scalar transport equations (stagnation enthalpy, temperature, or mass concentration) it represents the appropriate non-dimensional effective transport coefficient. The S_φ term represents the collective of all source and sink terms for the dependent variable in question.

If we redefine the diffusion term of this equation to be
then the generalized transport equation becomes

          The (x,y) to (x,ψ) Transformation - The independent variables in this generalized equation are now transformed from (x,y) to (x,ψ) coordinates using the following derivative transformation operators

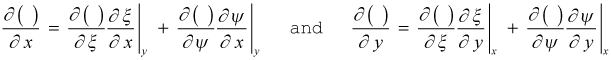
Now, evaluate the independent variable derivatives within these two derivative transformation operators, recalling that ξ = x, and it is orthogonal to y

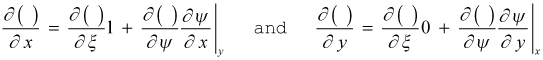
Now, introduce the stream function, ψ , to define the von Mises stream-function transformation that identically satisfies the variable-density conservation of mass,

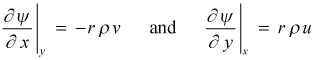
The final form of the derivative operators become

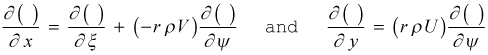
Now, transform the generalized boundary layer equation, preserving the ξ variable for clarity
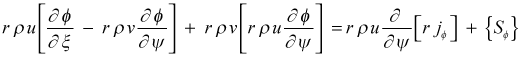
or

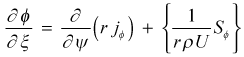
          The (x,ψ) to (x,ω) Transformation - The independent variables in this generalized equation are now transformed from (ξ,ψ) coordinates (ξ = x) to (η,ω) coordinates (η = x)using the following derivative transformation operators

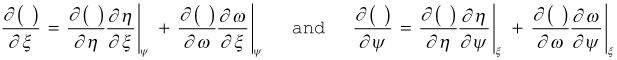
Now, evaluate the independent variable derivatives within these two derivative transformation operators, recalling that η = ξ = x, and they are all orthogonal to ψ

Define the non-dimensional stream function, ω , bounded by the stream function values at the domain bounding I-surface and E-surface. For an external boundary layer flow over a flat or curved I-surface is a solid surface and the E-surface is the free stream; for internal pipe flows, the I-surface is a symmetry line and the E-surface is a solid surface.

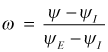
The derivative of ω with respect to ξ is
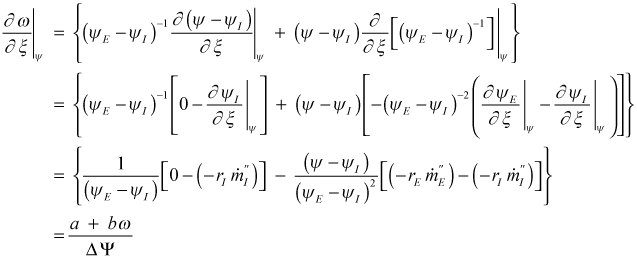
where
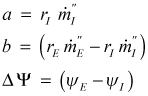
and the derivative of ω with respect to ψ is

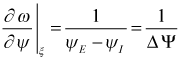
The final form of the derivative operators become

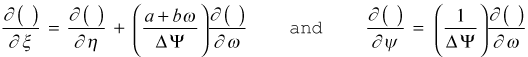
Transformation of the generalized equation to the (x,ω) coordinate system is straightforward. For simplicity, replace both the ξ and η variables by x, and the finalized form becomes

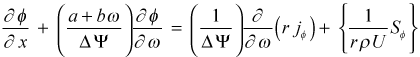
Numerical Solution Procedure - Solution to the generalized φ-equation is carried out using a form of the method of finite differences based on a finite volume formulation. The solution domain is bounded between two surfaces called the I- and E-surfaces in the cross-stream direction and the x location where the initial conditions are specified. This domain is called a parabolic domain, from the mathematics, because it is unbounded in the flow direction.

To obtain the solution, four basic steps are required:

1. subdivide the solution domain in the cross-flow direction into numerous sub-domains, called finite volumes
2. for each finite volume, identify a location within the volume that will represent the dependent variable (φ)
3. develop an algebraic equation that links this dependent variable to the values of the dependent variables that are in the neighboring finite volumes
4. solve the set of algebraic equations to determine φ(x,ω) and then transform it back to φ(x,y)

Because the problem is parabolic, the two-dimensional solution can be started at any initial x location and marched in the x-direction, rather than having to solve for the complete (x,y) field as is required for, say, two-dimensional conduction heat transfer problems. Typical starting x locations would be close to the leading edge of a flat plate for the Blasius problem or at the entrance for a pipe-flow problem. Note that external flows can not be started at a singularity where the velocity field is zero because of the nature of the von Mises transformation.

There exists several methods to develop the algebraic equation that links the dependent variable to its nearest neighbors. With each of these methods the governing differential equations are replaced with difference equations, which become the algebraic equations for solution.

The method of Patankar¹ is used in TEXSTAN to integrate the governing differential equation over a finite volume. This method creates integrals for each term of the differential equation, and to carry out the integration, one or more assumption(s) must be made as to how the variable φ_i will vary in the cross-stream direction. Based on these assumption(s) each integral is evaluated, and the result is a linearized algebraic equation for each node location i.

These equations are then assembled into a set and solved by a tri-diagonal matrix algorithm, and iterated as needed. Boundary conditions on the set of difference equations depends on whether their mathematical form is Dirichlet or Neumann.

References