mixing length model

Summary - The mixing length formulation in TEXSTAN is the classical Prandtl model
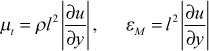
and the complete formulation of the mixing length is
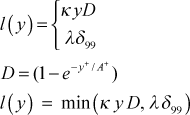
where D is the Van Driest damping function; A⁺ is the sublayer damping constant; y⁺ is the nondimensional distance from the wall in wall coordinates; u_τ is the shear velocity or friction velocity; and the mixing-length model constants are κ, the von Karman constant, and λ, the outer-layer constant. For external flows the boundary layer thickness δ₉₉ is the edge of the boundary layer where (u/u_∞)=0.99 . This value is formulated to exclude localized maximums within the boundary layer. For internal flows, the del99 for pipe flow (kgeom=4) is the wall radius, for parallel-plane channel flow (kgeom=5,6) it is the channel half height, and for annular flow (kgeom=7), it is arbitrarily set equal to the average of the inner and outer radius.

For circular pipes and parallel planes internal flows, there is a hybrid scheme where the mixing length model is applied in the near-wall region and a constant eddy diffusivity is applied in the outer flow,
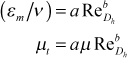
where a and b are model constants and Re_Dh is the hydraulic diameter Reynolds number. .

The flag ktmu identifies the model for computing the turbulent viscosity. The table below presents a summary of the mixing length model constants used in TEXSTAN for the various ktmu choices. Note that models ktmu =2 and =8 permit the user to change the model constants with input variables axx, bxx, cxx, dxx, exx.

ktmu	turbulence model choices for external boundary layer flows
=1
=2
=3
=4
=5

ktmu	turbulence model choices for internal flows
=6
=7
=8

External Flows - For external boundary layer flows, the functional form of A⁺ follows the model developed in our textbook CHMT
where A_∞⁺ is a model constant; p⁺ is the nondimensional pressure gradient parameter in wall coordinates; v_s⁺ is the nondimensional wall transpiration parameter in wall coordinates; and the other model constants are a=7.1 (=9.0 if <0), b=4.25 (=2.9 if p⁺v>0), and c=10.0 (=0 if p⁺>0).

The A⁺ function represents the sublayer and it is affected by wall boundary condition changes due to transpiration or roughness, and to momentum sources that are distributed within the boundary layer, such as the pressure gradient. Experimental evidence suggests the sublayer response to boundary condition or source changes is not instantaneous, and a new state of sublayer equilibrium is not completely established for some distance along the surface.

Thus a lag equation could be used to delay changes to A⁺ when p⁺ and/or v_s⁺ change with x,
where A_eq⁺ is the equilibrium value that would be determined from the A⁺(p⁺,v_s⁺) function based on the local p⁺ and/or v_s⁺; x⁺ is the nondimensionalized flow distance in wall coordinates; and d is an empirical constant.

A second method of reflecting the change of the sublayer thickness is to reformulate the A⁺ function as follows
where the effective values of p⁺ and v_s⁺ are computed using the scheme based on the A⁺ lag equation described above. For example, the lag equation for p⁺ is
which upon integration becomes
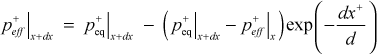
where dx⁺ is the nondimensional integration step converted to wall coordinates and d = 4000. This value is reduced to d = 1200 if the equilibrium value exceeds the effective value. With acceleration and blowing, the effective value of p⁺ can not be more negative than -0.032. A similar equation is used for computing the effective value of v_s⁺.

TEXSTAN uses this second method, and A_eff⁺ replaces A⁺ in the mixing length model, with no change in model constants.

The model for the outer layer length scale parameter λ has a low Reynolds number behavior and a behavior that reflects the wall boundary condition (transpiration or surface roughness). The correlation used in TEXSTAN is based on the momentum thickness Reynolds number and the transpiration,
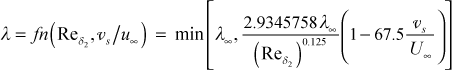
where λ_∞ = 0.085 and the momentum Reynolds number is ≤5500. Note that the ratio of wall transpiration velocity to free stream velocity is the same as the wall mass flux to the free stream mass flux for constant properties.

Internal Flows - For internal flows, there are two model choices for formulating the turbulent viscosity. The first choice is to apply the external flow mixing length model over the entire internal flow (wall to centerline for kgeom=4,5 and wall to wall for kgeom=6,7), and the second choice is a hybrid scheme where the mixing length model is applied in the near-wall region and a constant eddy diffusivity is applied in the outer flow. When the mixing length model is being applied to internal flows, λ = λ_∞ and A⁺ = A_∞⁺ values are used, rather than the functionals that are used with external flows.

The constant diffusivity model is only tested for circular pipes and parallel planes, and it is given by
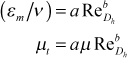
where a and b are model constants and Re_Dh is the hydraulic diameter Reynolds number. The constant turbulent viscosity model is applied when μ_t based on the inner layer formulation of the mixing length (κyD) exceeds the μ_t based on the constant diffusivity model. For pipes, a=0.005 and b=0.9, and for parallel-planes channels, a=0.0022.

For internal flows there is a choice of either a pure mixing-length model or a hybrid mixing-length and constant eddy diffusivity model. The mixing-length model incorporates the van Driest damping function, with the A⁺ being a constant value. For the hybrid model a constant eddy diffusivity for momentum is computed as a function of hydraulic diameter Reynolds number for the outer layer away from a wall. The outer layer model is used when its value exceeds the mixing-length model value or when the distance from the wall exceeds a certain value. This hybrid model is valid only for fully-developed pipe flow and fully-developed flow between parallel planes. A model for roughness can also be used in conjunction with the mixing-length model.