heat transfer

Convective heat transfer occurs within a fluid wherever a wall temperature gradient exists. The most common way of establishing a temperature gradient within a wall-bounded external flow is to make the wall temperature be different from the free stream static temperature of the fluid flowing over the wall. Another way of creating temperature gradients within a fluid is from the effects of viscous dissipation, and this occurs either with high-speed flows at any Prandtl number or with low-speed high-Prandtl number flows.

Sign Convention for External Heat Transfer - The solid surface for all external flow geometries (kgeom=1,2,3) is the I-surface and the corresponding E-surface is the free stream. The +y direction coordinate extends outward into the fluid from this no-slip I-surface. A positive heat flux boundary condition value means the boundary layer fluid is being heated by the wall, and a negative value means the boundary layer fluid is being cooled by the wall. Based on this definition, Fourier's law will have a minus sign.

Heat Transfer in Constant Property Flow - When constant properties are being considered, the stagnation enthalpy equation reduces to the temperature equation. The wall heat transfer is computed using the heat flux formulation of Fourier's law of heat conduction. The heat transfer coefficient is then defined by equating Fourier's law to Newton's law of cooling and recast into a nondimensional form using two traditional choices: the convection-based Stanton number and the conduction-based Nusselt number. The following is the calculation sequence used in TEXSTAN

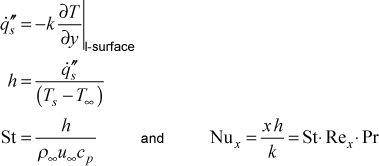
Heat Transfer in Variable Property Flow - The effects of variable properties on heat transfer are generally due to one of two reasons: high speed flow (Mach number > 0.4 causing significant viscous dissipation, especially in the near-wall region where the velocity gradients are very large) or flows with large temperature differences. When variable properties are being considered, the thermal energy equation in TEXSTAN is the stagnation enthalpy, and the heat transfer coefficient is defined based on the difference between the wall temperature and the free stream stagnation temperature. The following is the sequence used in TEXSTAN for computing the heat flux using the conduction rate equation (Fourier's law), the heat transfer coefficient using the convection rate equation (Newton's law of cooling), and the nondimensional Stanton and Nusselt number parameters
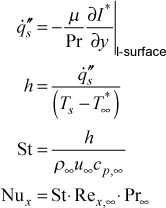
Note, the difference between using the stagnation enthalpy gradient and the static enthalpy gradient in Fourier's law is negligible because the velocity in this near-wall region is almost zero. All properties in the nondimensional quantities are evaluated at the free stream static conditions. The subscript "p" is added to the specific heat because this formulation is used mostly for gases.

By use of the flag k2 the definition of the heat transfer coefficient can be easily switched from being based on the stagnation temperature to the adiabatic wall temperature (or recovery temperature), (T_s - T_aw), where the stagnation temperature and adiabatic wall (or recovery) temperature definitions are

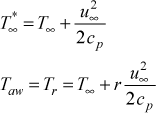
The recovery factor, r, for k2=1 is based on whether the flow is laminar or turbulent, r = Pr^1/2 for laminar flow (mode=1) and r = Pr^1/3 for turbulent flow (mode=2). For k2=3 the recovery factor is fixed at r = 0.892.