curvature

Curvature effects in TEXSTAN are limited to the mixing length and 1-equation models of turbulence for external flows only, and no additional curvature terms are added to the governing equations. The curvature model is developed in detail in our textbook CHMT, and in Adams and Johnston¹. The model is switched on for the mixing length by the input variable kbfor=5. Note that these models have received limited testing.

The radius of curvature is input using the input variable array aux3(m) and the array is linearly interpolated to obtain R(x). It is imperative that this distribution be smooth, and it can be checked using the k8=36 diagnostic check. At each x-location, the radius of curvature is inverted to formulate the local surface curvature, K_eq = 1/R, and a damping function controls the rate of change of the curvature. An effective curvature is then created using the same idea that was described in the mixing length model section for damping A⁺, primarily because of how strongly the curvature effect can be on the sublayer and its response to change,
which upon integration becomes
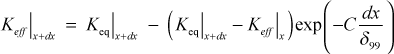
where C=0.20. This effective curvature is then converted back into an effective radius of curvature, R_eff = 1/K_eff.

Using this effective radius of curvature the sublayer A⁺ value in the Van Driest damping function is modified
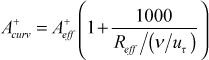
Note, R_eff < 0 will be concave curvature and R_eff > 0 will be convex curvature. Thus, concave surfaces will reduce the sublayer thickness (raising the c_f /2 and St) and convex will increase the sublayer thickness and have the opposite effect.

To implement the curvature model the mixing length distribution is computed using the non-curvature form of the outer layer constant and the curvature-modified sublayer A+ constant.

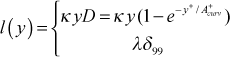
We know that a major effect of curvature is in the outer layer of the boundary layer, and this will be related to overall modification of the mixing length. The Richardson number at a value y, is formulated as

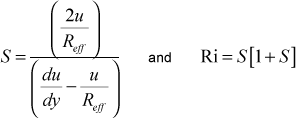
For convex curvature, R_eff > 0, causing the Richardson number to be positive, and the mixing length for the inner region of the boundary layer is then modified using

Now a curvature-modified outer-region mixing length constant is formulated and an outer-layer mixing length is calculated

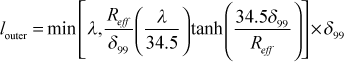
This value is compared to the curvature-modified inner-region mixing length and the smaller value is chosen

For concave curvature, R_eff < 0, causing the Richardson number to be negative. For this curvature a simple curvature correction is used to modify the mixing length
which leads to a mixing length increase due to the unstabilizing concave curvature.

Note that the mixing length is tested to require that it monotonically increase with y for the curvature model.

References