construction of the dataset

The contents of the laminar boundary layer benchmark dataset, s10.dat.txt, is described in four data blocks:

Data Block ONE - Geometry, PDE's, Models, Units, and Fluid

###1

'title of dataset'
s10.dat, lam, Blasius, Ts(x)

• title - to appear in all output files

This is a descriptive user-written alphanumeric statement of 80 characters maximum

###2

kgeom	neq	kstart	mode	ktmu	ktmtr	ktme
1	2	4	1	0	0	0

• kgeom - flag for the type of geometry

=1   is a flat plate geometry (no radius of transverse curvature or radius of curvature in the flow direction). This is the Blasius geometry.

Note that for planar geometries TEXSTAN computes the flow on a per unit width basis, so the surface width is not be a required input variable. Integration of the heat flux to determine total heat transfer or surface shear stress to determine shear drag will require multiplying the result by the value of the surface width.

• neq - flag for the number of transport equations to be solved

=2   means TEXSTAN will solve the momentum transport equation and one other transport equation. The problem statement specifies investigation of friction and heat transfer characteristics of the Blasius flow. Therefore two equations need to be solved (momentum and energy).

The Blasius flat plate problem could be considered either a pure momentum problem (friction) or it can be considered a combined momentum and heat transfer problem. The flag that will define the "other transport equation" is the variable jsor. For the Blasius problem the user will choose jsor =1 and that will tell TEXSTAN that the second transport equation is a thermal energy equation.

Note that if the Blasius solution for momentum is all that is required, setting neq =1 will eliminate solution to the thermal energy equation.

• kstart - flag to specify the type of initial profiles and whether they will be TEXSTAN-generated or input from tables

=4   instructs TEXSTAN to compute laminar initial profiles for velocity and temperature, derived from the Blasius solution, to start the calculations. Note the temperature profiles will be valid in the range of fluids for gases and light liquids.

• mode - flag to tell TEXSTAN whether to compute turbulent viscosity at the start of the calculations

=1   means the flow will start laminar, which is correct for the Blasius laminar flow problem.

• ktmu - the flag to tell TEXSTAN what to use for a momentum equation turbulence model

=0   This flag value means the flow will remain laminar because no turbulence model is specified for possible transition to turbulent flow.

• ktmtr - the flag to tell TEXSTAN what to use for a transition turbulence model

=0   tells TEXSTAN turbulent transition is not permitted for this Blasius flow.

• ktme - flag to tell TEXSTAN what to use for an energy equation turbulence model

=0   This value is consistent with ktmu =0 even though heat transfer is being considered.

###3

kbfor	jsor(1)	jsor(2)	jsor(3)	jsor(4)	jsor(5)
1	1

• kbfor - the flag to tell TEXSTAN what body forces to include in the momentum equation source term

=1   means only the pressure gradient, dp/dx, will be calculated as a momentum source term. This value is used for most flow problems unless free convective body forces are also being considered.

The Blasius problem is a special flow case requiring u_∞= constant, so the computed pressure gradient will be zero for all x.

• jsor(j) - the flag to tell TEXSTAN what each diffusion equation will be and which set of source terms to include when formulating the general source for this diffusion equation

jsor(j=1)=1    The problem statement tells us that heat transfer is being considered, so the jsor(j=1) value will have to be in the range between 1-8. In this range TEXSTAN knows this diffusion equation is the energy equation, and by setting the value =1 we tell TEXSTAN not to compute energy source terms for viscous dissipation or work against body forces.

jsor(j=2) - jsor(j=5) flags will be left blank because neq=2 for this Blasius problem, meaning only (neq-1)=1 diffusion equations will be solved and TEXSTAN will not need to read the other array values.

###4

kfluid	kunits
1	1

• kfluid - the flag to tell TEXSTAN whether to use constant or variable properties

=1   is the choice for constant properties, a requirement for the Blasius problem.

• kunits - the flag to tell TEXSTAN whether to use SI (metric) units or U.S. Customary (English/British) units for all physical variables

=1   is the choice to use SI units.

###5

po	rhoc	viscoc	amolwt	gam/cp
1013325.0	1.17700	1.838E-05	00.00	1005.00

• po - the fluid pressure at the start of computations, x = xstart

=101325.0   in units of N/m² or Pa - (atmospheric pressure) - the fluid pressure will be interpreted as static pressure rather than total pressure because of the constant properties assumption, kfluid =1.

• rhoc - the fluid mass density

=1.17700    in units of kg/m³ - (air at about 325 K and one atmosphere).

• viscoc - the fluid dynamic viscosity

=1.935E-05    in units of (N-s)/m² or (Pa-s) - (air at about 325 K).

• amolwt - the fluid molecular weight

=00.00    variable not required for constant property calculations - TEXSTAN input format does not permit a blank for a zero value.

• gam/cp - the ratio of the fluid specific heats (or) the fluid specific heat

=1005.00   in units of J/(kg-K) - (specific heat at constant pressure for air at about 325 K) - the variable is interpreted as the fluid specific heat, rather than gamma, the ratio of specific heats, because of the constant properties assumption, kfluid =1.

###6

prc(1)	prc(2)	prc(3)	prc(4)	prc(5)
0.707

• prc(j) - generalized transport equation C variable for each diffusion equation

prc(j=1)=0.707   TEXSTAN interprets prc(j=1) as a Prandtl number (in this problem Pr for air at about 325K) because jsor(j=1) was set =1 (meaning the first diffusion equation is an energy equation).

prc(j=2) - prc(j=5) flags will be left blank because neq=2 for this Blasius problem, meaning only (neq-1)=1 diffusion equations will be solved and TEXSTAN will not need to read the other array values.

Data Block TWO - Boundary Conditions

###7 (and) ###8

nxbc(I)	jbc(I,1)	jbc(I,2)	jbc(I,3)	jbc(I,4)	jbc(I,5)
5	1

nxbc(E)	jbc(E,1)	jbc(E,2)	jbc(E,3)	jbc(E,4)	jbc(E,5)
5	1

• nxbc(I) - number of boundary condition locations, I-surface

nxbc(I)=5    indicates there will be a total of five x-locations where boundary conditions are specified. We could use two (the minimum number) because there is no variation in either the free stream velocity or surface temperature for the Blasius problem. The extra three boundary conditions are provided only for ease in obtaining velocity and temperature profiles when the k10 variable is reset =10 or =11.

• nxbc(E)=nxbc(I) - number of boundary condition locations, E-surface

nxbc(E)=5    This value must be identical to nxbc(I)

• jbc(I,j) - the flag to tell TEXSTAN type of boundary condition at the I-surface (Dirichlet or level, Neumann or flux, or symmetry line) for each diffusion equation

jbc(I,j=1)=1   tells TEXSTAN that the boundary condition along the I-surface for the first diffusion equation (the energy equation) will be mathematically a Dirichlet or level type, which translates into a surface temperature distribution along the I-surface (if it had been =2, it would have been mathematically a Neumann or flux type, which would imply a surface heat flux distribution along the I-surface).

jbc(I,j=2) - jbc(I,j=5) flags will be left blank because neq=2 for this Blasius problem, meaning only (neq-1)=1 diffusion equations will be solved and TEXSTAN will not need to read the other values in the array.

• jbc(E,j) - the flag to tell TEXSTAN type of boundary condition at the E-surface (Dirichlet or level, Neumann or flux, or symmetry line) for each diffusion equation

jbc(E,j=1)=1   tells TEXSTAN that the boundary condition along the E-surface for the first diffusion equation (the energy equation) will be mathematically a Dirichlet or level type, which translates into a free stream temperature. Note that TEXSTAN will use the input variable tstag to specify the free stream temperature.

jbc(E,j=2) - jbc(E,j=5) flags will be left blank because neq=2 for this Blasius problem, meaning only (neq-1)=1 diffusion equations will be solved and TEXSTAN will not need to read the other values in the array.

###9

x(m)	rw(m)	aux1(m)	aux2(m)	aux3(m)
0.0000000	1.0000	0.0000	0.0000	0.0000
0.0500000	1.0000	0.0000	0.0000	0.0000
0.1000000	1.0000	0.0000	0.0000	0.0000
0.1500000	1.0000	0.0000	0.0000	0.0000
0.2000000	1.0000	0.0000	0.0000	0.0000

• x(m) - the boundary condition x-location array

As seen in the x(m) array table, there are five points, including x(1)=0.0 and x(5)=0.2 (the plate length in meters for this Blasius problem). As indicated in the definition of nxbc we could use two (the minimum number) because there is no variation in either the free stream velocity or wall temperature for the Blasius problem. The extra three boundary conditions are provided only for ease in obtaining velocity and temperature profiles when the k10 variable is reset =10 or =11.

• rw(m) - the transverse curvature array that contributes to defining a given geometry

As seen in the rw(m) array table, these values are arbitrarily set =1.0 because the Blasius problem is flow over a flat plate (kgeom=1) which is a planar surface. The transverse radius divides out of the axisymmetric-formulated transport equations.

• aux1(m) - an auxiliary array that is used to provide additional input data to TEXSTAN

As seen in the aux1(m) array table, this variable is not required for the Blasius problem, but it must be filled with zero values because it is part of the structured data input for TEXSTAN.

• aux2(m) - an auxiliary array that is used to provide additional input data to TEXSTAN

As seen in the aux2(m) array table, this variable is not required for the Blasius problem, but it must be filled with zero values because it is part of the structured data input for TEXSTAN.

• aux3(m) - an auxiliary array that is used to provide additional input data to TEXSTAN

As seen in the aux3(m) array table, this variable is not required for the Blasius problem, but it must be filled with zero values because it is part of the structured data input for TEXSTAN.

###10

ubI(m)	am(I,m)	fj(I,1,m)	fj(I,2,m)	fj(I,3,m)	fj(I,4,m)	fj(I,5,m)
ubE(m)	am(E,m)	fj(E,1,m)	fj(E,2,m)	fj(E,3,m)	fj(E,4,m)	fj(E,5,m)
0.00	0.000	295.0
15.00	0.0	0.0
0.00	0.000	295.0
15.00	0.0	0.0
0.00	0.000	295.0
15.00	0.0	0.0
0.00	0.000	295.0
15.00	0.0	0.0
0.00	0.000	295.0
15.00	0.0	0.0

• ubI(m) - the momentum flow-direction velocity boundary condition array at the I-surface

The ubI(m) array for external flows (kgeom=1,2,3) is the no-slip velocity boundary condition at the solid surface, and all values are set =0.00.

• ubE(m) - the momentum flow-direction velocity boundary condition array at the E-surface

The ubE(m) array for external flows (kgeom=1,2,3) is the free stream velocity boundary condition at the solid surface, and all values are set =15.00. This constant free stream velocity is required for the Blasius problem.

• am(I,m) - the momentum cross-stream mass flux boundary condition array at the I-surface

The am(I,m) array for external flows (kgeom=1,2,3) is the wall transpiration (cross-stream or y-directed mass flux) at the solid surface, and all values are set =0.000 for the Blasius problem.

• am(E,m) - the momentum cross-stream ( or y-directed) mass flux boundary condition array at the E-surface

The am(E,m) array for external flows (kgeom=1,2,3) would be the cross-stream (y-directed) mass flux at the free stream. All values are set =0.0 for any external flow because it can not be prescribed as a boundary condition. Note that it can not be left blank because it is part of the structured data input for TEXSTAN.

• fj(I,j,m) - the diffusion equation boundary condition array at the I-surface for each j at each x(m) location

Recall that there will be (neq-1) diffusion equations and each equation is uniquely identified by its jsor(j) value. Furthermore, the type of boundary condition is uniquely identified as either a Dirichlet (level) type or a Neumann (flux) type by its jbc(I,j) value.

For the Blasius problem, jsor(j=1) =1 means it is an energy equation and jbc(I,j=1) means the boundary condition is Dirichlet (surface temperature distribution). Therefore, from the table entries fj(I,j=1,m) = 295.0 is the surface temperature in degrees Kelvin.

fj(I,j=2,m) - fj(I,j=5,m) variables will be left blank because neq=2 for this Blasius problem, meaning only (neq-1)=1 diffusion equations will be solved and TEXSTAN will not need to read fj(I,j=2,m) - fj(I,j=5,m).

• fj(E,j,m) - the diffusion equation boundary condition array at the E-surface for each j at each x(m) location

For external flows, the E-surface represents a free stream, and the fj(E,j,m) variable is only used to specify the free stream value of the mass diffusion equation. For the energy equation, it is specified by the tstag variable and for the turbulence model equations it is computed by integration of the model equations in their reduced free-stream form. For the energy equation and the turbulence model equation(s) E-surface values are set =0.0. Note that they can not be left blank because they are part of the structured data input for TEXSTAN. Thus, for the Blasius problem, from the table entries fj(E,j=1,m) are set = 0.0 (and instead tstag will be set =300.0 K for the free stream temperature).

fj(E,j=2,m) - fj(E,j=5,m) variables will be left blank because neq=2 for this Blasius problem, meaning only (neq-1)=1 diffusion equations will be solved and TEXSTAN will not need to read fj(I,j=2,m) - fj(I,j=5,m).

Data Block THREE - Integration and Print Control

###11

xstart	xend	deltax	fra	enfra
0.0010410	0.200000	0.100	0.010	1.000E-06

• xstart - the location for the start of computations, x = xstart

=0.0010410   in units of m. We often determine xstart by first assuming a x-Reynolds number for the start of computations and then back-calculate what x will be needed to achieve this Re. For the Blasius problem, the choice for xstart leads to a starting Re of about 1000.

Note that there is nothing to be gained by choosing a lower starting x-Reynolds number in terms of numerical accuracy, and there is strong negative effect, namely that there can be an enormous increase in number of integration steps because the integration stepsize is proportional to the boundary layer thickness. For flow over a flat plate x = xstart = 0.0 is not an option (due to the von Mises numerical transformation issue).

• xend - the location for the end point of computations, x = xend

=0.2000000   in units of m. The two typical choices for xend are to let xend = x(nxbc) and to let xend be a defined x-Reynolds number. For the Blasius problem, the choice for xend is x(nxbc), the plate length, which leads to an end-point Re of about 2E+05.

Note, a reminder that the plate width never enters the numerical formulation of the equations within TEXSTAN. All computations are per unit span (width) for planar geometries and per unit radian for axisymmetric geometries. Also note that the plate length can lead to any value of x-Reynolds number (even unrealistically large values) and the flow will remain a laminar computation as long as the user has set mode=1, along with ktmu=0.

• deltax - the nondimensional integration stepsize variable

=0.100    (dimensionless). This is a recommended value for laminar flows in which there is no abrupt changes in thermal boundary conditions (such as an unheated starting length). The value was determined by exhaustive testing of this Blasius benchmark dataset and comparison with the Blasius analytical results. Note this comparison is shown in the benchmark-formulated output file because kout is set =8.

• fra - the nondimensional variable that contributes to limiting integration stepsize

=0.010    (dimensionless). This is a recommended value for laminar flows. It is part of the set of integration controls for external flows, and it is designed to limit stepsize in the event that the boundary layer grows too fast. Recall the deltax variable makes integration stepsize proportional to the boundary layer thickness, and a strong increase in that thickness leads to an increase in physical integration stepsize, which generally results in a perceived need to further increase entrainment. The entrainment in turn causes the boundary layer to grow, and this potentially negative feedback loop is limited by fra. Typically this variable is activated only for adverse pressure gradient flows or free-convective boundary layers, and thus not applicable to the Blasius problem.

• enfra - the nondimensional variable that contributes to limiting integration stepsize

=1.000E-06    (dimensionless). This is a recommended value for laminar flows. It is part of the set of integration controls for external flows, and it is designed to help ensure the derivatives of dependent variables (the variables are identified by the flag kent) will be as close to zero as possible as they approach the edge of their respective 99-percent boundary layer thicknesses. The value was determined by exhaustive testing of this Blasius benchmark dataset and comparison with the Blasius analytical results. For the Blasius problem, where the free stream velocity is constant, a value on the order of 1.000E-06 is more than sufficient, and for pressure-gradient flows where the boundary layer thicknesses are continuously changing, this is generally too strict.

###12

kout	kspace	kdx	kent
8	100	0	1

• kout - flag to tell TEXSTAN which formatted output routine to use for the file out.txt

=8    This choice has a format designed to accompany benchmark datasets. The choice kout =2 can also print external flows. The file out.txt is used primarily for an overview of the integration results, and it is not formatted for data analysis. The integration results are reformatted into a series of ftn.txt files for this purpose, and these files will be written when the flag k5 is set > 0.

• kspace - flag to choose the interval for printing integration steps in the file out.txt

=100    This choice means that every 100 integration steps a line of output will be written. This flag is very useful for controlling the overall size of the file out.txt, especially for printing purposes.

• kdx - flag to cause TEXSTAN to bypass the use of the deltax variable for integration stepsize control and instead use interpolated values from the aux1(m) array

=0    This choice means TEXSTAN will use the deltax variable for integration stepsize control.

• kent - flag for external flows onto tell TEXSTAN which dependent variables to examine for numerical accuracy related to entrainment

=1    This choice means TEXSTAN will monitor the near free stream derivatives of both the momentum (velocity) boundary layer and the energy (temperature for the Blasius problem) boundary layer, and changes to entrainment will be based on whichever boundary layer has a derivative that is becoming too large. Again, for the Blasius problem, kent=1 is especially important because the fluid Prandtl number is < 1, and the thermal boundary layer will be larger than the velocity boundary layer. Choosing kent=0 (entrainment based only on the velocity boundary layer) will result in numerical accuracy problems.

###13

k1	k2	k3	k4	k5	k6
0	0	0	0	50	0

• k1 - flag is not used

• k2 - flag is not used

• k3 - flag is not used

• k4 - flag is not used

• k5 - flag to choose the interval for printing integration steps in various ftn.txt files

=50    When the flag is set >0 various ftn.txt files will be printed that contain arrays of data for plotting, and the data will be printed at multiples of k5 integration steps (this flag functions exactly the same as the kspace flag for setting the print interval of out.txt). By control of the size of k5 the user can match the requirements of a plotting package (in terms of maximum number of data points for display). Descriptions of the ftn.txt files for external flows and their contents are given in the external flows: output files section of this website.

• k6 flag is not used

###14

k7	k8	k9	k10	k11	k12
0	00	0	0	0	0

• k7 - flag is not used

• k8 - flag is not used

• k9 - flag is not used

• k10 - flag is not used - note that it can be reset to print velocity and temperature profiles according to the k10 definition. Because the Blasius flow is a benchmark dataset, the k10=10 option presents profiles in the nondimensional Blasius variables to examine the self-similar nature of the solution.

• k11 - flag is not used

• k12 - flag is not used

###15

axx	bxx	cxx	dxx	exx	fxx	gxx
0.000E+00	0.000E+00	0.000E+00	0.000E+00	0.000E+00	0.000E+00	0.000E+00

• axx = 0.000E+00

• bxx = 0.000E+00 - note that if k10 is set =21,22,23 (to print one set of velocity and temperature profiles), then this variable will be set according to the k10 definition.

• cxx = 0.000E+00

• dxx = 0.000E+00

• exx = 0.000E+00

• fxx = 0.000E+00

• gxx = 0.000E+00

Data Block FOUR - Initial Conditions

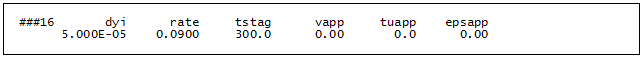
###16

dyi	rate	tstag	vapp	tuapp	epsapp
5.000E-05	0.0900	300.0	0.00	0.0	0.00

• dyi - this variable is used in the construction of the y spacing for the velocity profile, which in turn controls the grid (finite difference mesh) for TEXSTAN

=5.000E-05    This value is recommended for laminar boundary layer flows and kstart=4. It is explained in considerable detail in the external flows: initial profiles sections of this website.

• rate - this variable is used in the construction of the y spacing for the velocity profile, which in turn controls the grid (finite difference mesh) for TEXSTAN

=0.0900    This value is recommended for laminar boundary layer flows and kstart=4. It is explained in considerable detail in the external flows: initial profiles sections of this website.

• tstag - this variable is the free stream temperature (static or stagnation, depending on kfluid and kgeom)

=300.0    This is the free stream temperature (degrees Kelvin) for the constant property (kfluid=1) external flow (kgeom=1) Blasius problem.

• vapp - this variable is the approach velocity for extracting the initial value of the free stream turbulence kinetic energy from the tuapp variable for use with one- and two-equation turbulence models

=0.00    This variable is not required because the Blasius problem is a laminar flow. Note that it can not be left blank because it is part of the structured data input for TEXSTAN.

• tuapp - this variable is the free stream turbulence intensity and it used to establish the initial value of the free stream turbulence kinetic energy for one- and two-equation turbulence models

=0.00    This variable is not required because the Blasius problem is a laminar flow. Note that it can not be left blank because it is part of the structured data input for TEXSTAN.

• epsapp - this variable establishes the initial value of the free stream turbulence dissipation for two-equation turbulence models

=0.00    This variable is not required because the Blasius problem is a laminar flow problem. Note that it can not be left blank because it is part of the structured data input for TEXSTAN.