Reynolds number

Hydraulic Diameter Reynolds Number - Internal flows use the hydraulic diameter Reynolds number for all flow geometries

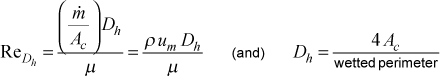
The variable A_c is the flow cross-sectional area, and the variable u_m is the mass-averaged velocity (which is the same as the mean velocity). The wetted perimeter depends on the flow cross-sectional area: for a pipe it will be the circumference, and for an annulus it will be the sum of the inner circumference and the outer circumference.

For a flat duct (sometimes called a parallel planes duct) the perimeter can be defined as two times the duct (or parallel planes) spacing plus two times a "large" variable that represents the width of the parallel planes, say L, which is theoretically infinite in length. When the ratio of cross-sectional area to wetted perimeter is formed, terms will form where L is in the denominator, and in forming the limit as L goes to infinity, those terms will vanish. For the flat duct the area-perimeter ratio becomes (L x a)/(2L + 2a) = (a)/(2 + 2a/L) = a/2, leading to a hydraulic diameter of 2a.

For variable properties, the thermophysical variables are evaluated at the mass-averaged temperature (which is the same as the mixed-mean temperature or the mean temperature or the bulk temperature).